filmov
tv
Solving Schrödinger's Equation as an Eigenvalue Problem with Numpy

Показать описание
Solving the 1D infinite square well using the finite difference method and the eigenvalue problem. In this example, I'm using python numpy
Here is another finite difference method using lists
Here is my analytical solution to the 1D infinite square well.
After that, I created a numerical solution in python using the shooting method.
Here is another finite difference method using lists
Here is my analytical solution to the 1D infinite square well.
After that, I created a numerical solution in python using the shooting method.
The Schrödinger Equation Explained in 60 Seconds
Quantum Mechanics and the Schrödinger Equation
SOLVING the SCHRODINGER EQUATION | Quantum Physics by Parth G
Schrodinger Equation. Get the Deepest Understanding.
Schrodinger Equation Explained - Physics FOR BEGINNERS (can YOU understand this?)
Schrödinger equation for hydrogen
How to Solve Schrödinger's Equation using Separation of Variables
Unpacking the Schrödinger Equation
Quantum chemistry, Schrodinger wave equation.
What is the Schrödinger Equation? A basic introduction to Quantum Mechanics
Particle in a Box Part 1: Solving the Schrödinger Equation
Solve Schrödinger Equation in Seconds with Python & GPU
Solving the Schrödinger equation
What is The Schrödinger Equation, Exactly?
The True Meaning of Schrödinger's Equation
Quantum Wavefunction | Quantum physics | Physics | Khan Academy
Solving the Schrodinger Equation | The Free Particle
Can I Explain the Schrödinger Equation in 60 Seconds? (reupload for #shorts)
SCHRÖDINGER'S EQUATION (Derivation) - Plausibility Argument & Time-Independent SE Derivatio...
Schrödinger Equation: Quantum in a Flash!
quantum mechanics 🌸#schrodinger equation
Time-Dependent Schrodinger Equation in Python: Two Different Techniques
The Hydrogen Atom, Part 2 of 3: Solving the Schrodinger Equation
Schrodinger equation solutions to the hydrogen atom
Комментарии
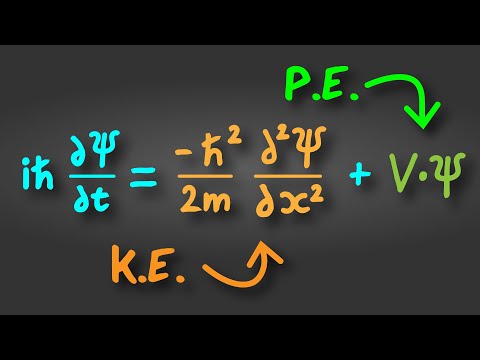 0:01:00
0:01:00
 0:06:28
0:06:28
 0:13:04
0:13:04
 0:49:30
0:49:30
 0:08:45
0:08:45
 0:20:59
0:20:59
 0:05:35
0:05:35
 0:14:13
0:14:13
 0:06:08
0:06:08
 1:27:34
1:27:34
 0:16:35
0:16:35
 0:33:23
0:33:23
 0:02:38
0:02:38
 0:09:28
0:09:28
 0:12:19
0:12:19
 0:10:11
0:10:11
 0:04:30
0:04:30
 0:01:00
0:01:00
 0:55:36
0:55:36
 0:00:14
0:00:14
 0:00:16
0:00:16
 0:25:18
0:25:18
 0:46:00
0:46:00
 0:17:27
0:17:27