Particle in a Box Part 1: Solving the Schrödinger Equation

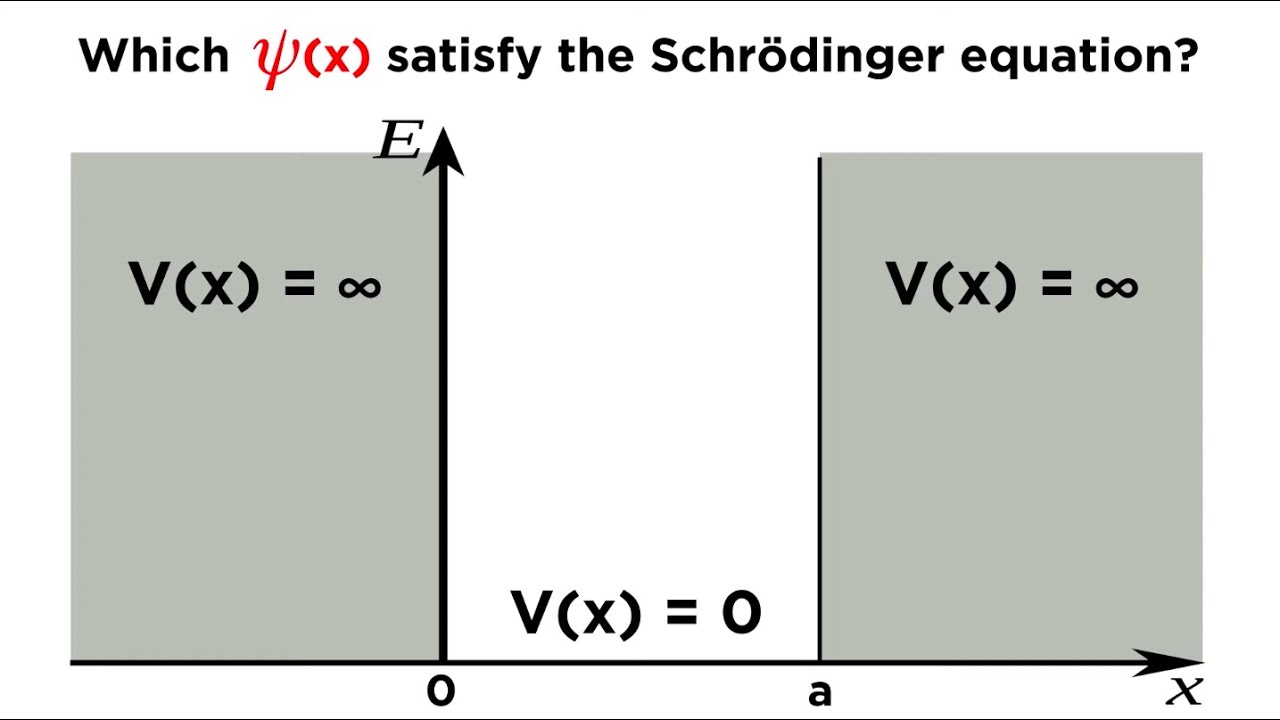
Now that we understand the Schrödinger equation, it's time to put it to good use, and solve a quantum problem. Let's find the eigenfunctions and eigenenergies associated with a quantum particle restricted to an infinite square well. This is also known as the famous "Particle in a Box" problem. It's not as hard as it sounds, check it out!

Script by Hèctor Mas

Check out "Is This Wi-Fi Organic?", my book on disarming pseudoscience!

[Felixkeeg]

Man, this brings back memories. This was one of the more satisfying things to do. Things being equal to zero and canceling out and ultimately arriving at a very clean solution is nice.

[matrixate]

I have to say...this is definitely well-scripted. Clearly, you've included the best parts of other videos and put it all together in one succinct, clear, and concise presentation. Honestly, it's about time someone did this. Thanks for making this available for everyone. I wish I would have had this when I took QM. It's all good...I had a lot of smart friends and grad students that were around to help clear things up.

[keithhammond]

I'll be starting my second quantum chemistry course in a few days, that was very helpful and couldn't have come at a better time. Thank you Professor Dave you rock as usual! Kudos from France

[zaynabhakim]

You are literally a lifesaver. Perhaps I should send this to my professor.

[duck]

Brings back memories from my undergrad

[Ai-ChingChen]

Prof Dave is truly amazing!!!
It's extremely clear and the steps are well-ordered to let us understand more easily.

[ishaangupta]

Man I couldn't understand anything from the slides I had, and all that maths was frightening. Thanks to you I am confident enough to try this by myself again. You are doing a great work please keep it up

[지구과학천문학]

oh god please tell me this is a series

[pranavlimaye]

I missed a whole bunch of physics lectures because of medical reasons. *I've never been more glad to be your subscriber....*
Thanks Professor Dave! <3

[TheRogueRockhound]

Not afraid to admit I need to go back to less advanced videos.
Thanks for taking the time to make these, I hope to purchase a mug or something in the near future.

[cgw]

Great video. You can prove that E≥0 and hence k is real by using that
E= <H> = <p²>/2m + <V> ≥ <V> ≥ min V(x) =0.
"If E=0 we don't even have a particle to begin with" Huh??? That rather depends on the potential. Just as in classical theory, if the potential energy is negative (admittedly not the case here), then E=0 is possible (e.g., parabolic orbits). You should rule out E=0 by the boundary conditions at x=0 and x=a (or show E=0 implies that <p²>=<V>=0 and <V>=0 implies that ψ=0.)

The quick way of getting the normalization is to remember that the average value of sin²(x) over an non-zero integer multiple of the half period is ½, Thus <ψ|ψ>= ½(length of interval)= ½a. Obviously, the reason why this works comes from the trig identity you quoted. This result is also useful when playing around with Fourier series.

[cguy]

I would like to point out that the entire equation could be solved strictly mathematically, and it really isn’t that difficult. I assume Dave is quite capable of doing this.

However, the way he used, by looking at how the terms look and behave is much more useful to someone learning it, because it helps you to visualize it. If you just went ahead and solved it, there are multiple places that errors could have crept in, and you would have no idea, ecause you would have no appreciation for what you were looking for.

Nice job!

[tonistar]

Thank you so much ! This is exactly what I am studying right now, and you make everything so much clearer and easier! Keep it up! I am waiting for your future videos of the series. :)

[charlesnathansmith]

This supplements the MIT OpenCourseware series really well. Both are great, but seeing the math broken down from a couple of different angles is really helpful

[williamcashion]

I've been looking at this and similar videos for maybe 6 years. Including the MIT series. Something about the way you presented this, I suddenly realized the integers ñ=2, n=3, etc, yielded the outer orbits. Thank you. Bill

[emlmm]

Maaan, I can't tell you how much I wish I'd had your videos back in Pchem.

[tommyottobisdee]

I’m staggered by how much clearer this is to understand than my university textbooks?! If only I could find a book that explains all of QM so clearly I’d have my module done in a few weeks, honestly!

I notice others have commented on how disarmingly simple the maths methods ultimately are here, and I’m inclined to agree…

However, there are so many sudden leaps from one equation to another, seemingly, on a whim in this topic - dividing by i, BUT being expected to use (-i), instead of 1/i, is a good example - that, if the situation just isn’t explained well, it gets baffling fast!

Thanks so much, easy sub from me 👍🏼

[light-and-thunder]

That was the most comprehensive and well explained solution of the infinite square well problem I ever seen! Thank you Professor Dave!

[codecmac]

how you made this simple is underrated, you resparked my interest in physics. thumbs up

[stephanietarczynski]

Great explanation! Sort of understood this in class but now I feel much more comfortable with it. Thank you so much.