filmov
tv
Linear Algebra 01: Prove a Matrix is Orthogonal (Ch1 Pr2)

Показать описание
This is Chapter 1 Problem 2 from MATH2501. Presented by Peter Brown.
Linear Algebra 01: Prove a Matrix is Orthogonal (Ch1 Pr2)
Vectors | Chapter 1, Essence of linear algebra
Gilbert Strang: Linear Algebra vs Calculus
Linear Algebra: Checking if a transformation is one-to-one and onto
Linear Algebra Determinant Proof det(A^(-1)) = (detA)^(-1)
Linear Algebra : Proof
The determinant | Chapter 6, Essence of linear algebra
Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra
Rank and Nullity of Linear Transformations | Linear Algebra
How to Find the Matrix of a Linear Transformation
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Eigenvectors and eigenvalues | Chapter 14, Essence of linear algebra
Proof Based Linear Algebra Book
Proof: Inverse of a Matrix is Unique | Linear Algebra
Inverse of a Transpose Matrix | Linear Algebra
Class 12th – Prove (AB) Inverse = B Inverse A Inverse | Matrices | Tutorials Point
Matrix multiplication as composition | Chapter 4, Essence of linear algebra
Matrices and Polynomials
This Will Help You With Linear Algebra
How to Prove a Set is a Subspace of a Vector Space
What does it mean for matrices to commute? | Linear algebra worked example
Linear Algebra 6.1.1 Inner Product, Vector Length and Distance
Linear Algebra Example Problems - Spanning Vectors #1
Linear Algebra for Beginners | Linear algebra for machine learning
Комментарии
 0:08:10
0:08:10
 0:09:52
0:09:52
 0:02:14
0:02:14
 0:06:29
0:06:29
 0:01:22
0:01:22
 0:04:21
0:04:21
 0:10:03
0:10:03
 0:12:09
0:12:09
 0:09:05
0:09:05
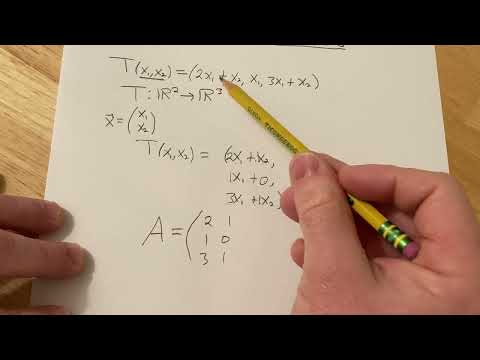 0:05:19
0:05:19
 0:10:59
0:10:59
 0:17:16
0:17:16
 0:00:24
0:00:24
 0:02:53
0:02:53
 0:03:54
0:03:54
 0:04:34
0:04:34
 0:10:04
0:10:04
 0:08:21
0:08:21
 0:00:52
0:00:52
 0:05:58
0:05:58
 0:07:14
0:07:14
 0:12:25
0:12:25
 0:04:31
0:04:31
 1:21:31
1:21:31