filmov
tv
GCD and Modular Inverse: Extended Euclidean Algorithm - Part 1

Показать описание
This video is the first part of a two-part video series that clearly explains the process of finding the greatest common divisor of two positive integers, and the inverse of a positive integer modulo another positive integer using the Extended Euclidean Algorithm. Please let me know your comments. Enjoy!!!
Extended Euclidean Algorithm and Inverse Modulo Tutorial
GCD and Modular Inverse: Extended Euclidean Algorithm - Part 1
How to compute the modular inverse of a number
GCD, Bezout, and Modular Inverses | The Extended Euclidean Algorithm
The Extended Euclidean algorithm
Extended Euclidean Algorithm (Solved Example 1)
GCD and Modular Inverse: Extended Euclidean Algorithm - Part 2
How To Find The Inverse of a Number ( mod n ) - Inverses of Modular Arithmetic - Example
Extended Euclidean Algorithm using Example Multiplicative inverse of a number | Cryptography
Extended Euclidean Algorithm Example
Multiplicative Inverse
CSS #15 Extended Euclidean Algorithm | GCD | Euclidean Algorithm | BTB | Multiplicative Inverse🔥
Modular Arithmetic and the Extended Euclidean Algorithm- Discrete Math Structures Lesson 7
Use Excel to find Modulo, GCD, and Modular Inverse
Asymmetric Cryptography, GCD, Euclidean Algorithm, Extended Euclidean Algorithms, Modular inverses
Modular inverse made easy
Finding the Multiplicative Inverse using Extended Euclidean Algorithm Example 1 HD
Extended Euclidean Algorithm - Example (Simplified)
How GCD and inverse are related?
Number Theory | Inverses modulo n
Extended Euclidean Algorithm to find multiplicative inverse| C implementation
Extended Euclidean Algorithm (Solved Example 2)
3.3 – Finding Modular Inverses
Extended Euclidean Algorithm (Solved Example 3)
Комментарии
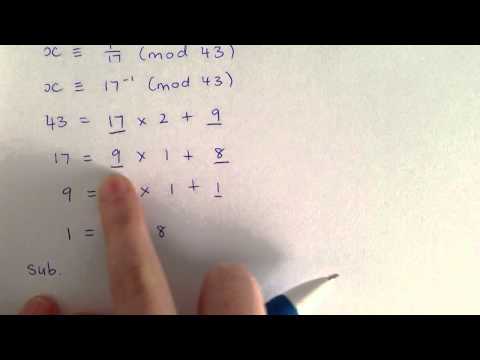 0:06:00
0:06:00
 0:44:48
0:44:48
 0:12:19
0:12:19
 0:22:21
0:22:21
 0:12:11
0:12:11
 0:10:16
0:10:16
 0:37:06
0:37:06
 0:10:58
0:10:58
 0:04:24
0:04:24
 0:14:50
0:14:50
 0:10:03
0:10:03
 0:13:01
0:13:01
 0:13:58
0:13:58
 0:21:30
0:21:30
 0:27:28
0:27:28
 0:04:12
0:04:12
 0:12:16
0:12:16
 0:07:40
0:07:40
 0:06:33
0:06:33
 0:08:02
0:08:02
 0:11:10
0:11:10
 0:05:43
0:05:43
 0:28:20
0:28:20
 0:06:54
0:06:54