filmov
tv
Number Theory | Extended Euclidean Algorithm Example #1

Показать описание
We use the extended Euclidean algorithm to write the greatest common divisor of two natural numbers as a linear combination of them.
The Extended Euclidean algorithm
Number Theory | Extended Euclidean Algorithm Example 2
Number Theory | Extended Euclidean Algorithm Example #1
Extended Euclidean Algorithm (Solved Example 1)
Extended Euclidean Algorithm Example
Number Theory: The Euclidean Algorithm Proof
Extended Euclidean Algorithm
Extended Euclidean Algorithm and Inverse Modulo Tutorial
Euclidean Algorithm - An example ← Number Theory
GCD, Bezout, and Modular Inverses | The Extended Euclidean Algorithm
Extended Euclidean Algorithm Explained
Extended Euclidean Algorithm
Number Theory 5 - Extended Euclidean Algorithm
EUCLIDEAN ALGORITHM - DISCRETE MATHEMATICS
An Example of GCD, and Extended Euclidean Algorithm In Finding the Bezout Coefficients
Extended Euclid Algorithm - Number Theory Advanced | C++ Placement Course | Lecture 37.1
Extended Euclidean Algorithm - Example (Simplified)
Number Theory - Extended Euclidean algorithm (Arabic)
How to Find the Greatest Common Divisor by Using the Euclidian Algorithm
Bézout's identity: ax+by=gcd(a,b)
Using Euclidean algorithm to write gcd as linear combination
Extended Euclidean Algorithm to Solve Linear Diophantine Equation
Extended Euclid’s Algorithm - Number Theory and Cryptography
[Number Theory 02] The Extended Euclidean Algorithm
Комментарии
 0:12:11
0:12:11
 0:12:13
0:12:13
 0:08:53
0:08:53
 0:10:16
0:10:16
 0:14:50
0:14:50
 0:05:50
0:05:50
 0:02:42
0:02:42
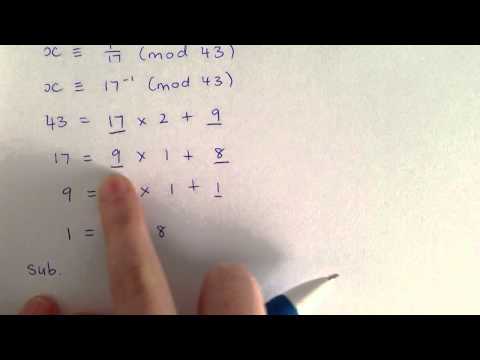 0:06:00
0:06:00
 0:02:04
0:02:04
 0:22:21
0:22:21
 0:06:21
0:06:21
 0:11:54
0:11:54
 0:05:19
0:05:19
 0:10:02
0:10:02
 0:00:59
0:00:59
 0:09:18
0:09:18
 0:07:40
0:07:40
 0:13:21
0:13:21
 0:04:10
0:04:10
 0:18:20
0:18:20
 0:08:31
0:08:31
 0:00:59
0:00:59
 0:10:10
0:10:10
![[Number Theory 02]](https://i.ytimg.com/vi/B5Cau43UAT8/hqdefault.jpg) 0:08:06
0:08:06