filmov
tv
A Quintic Diophantine Equation (x^5-y^5=1993)
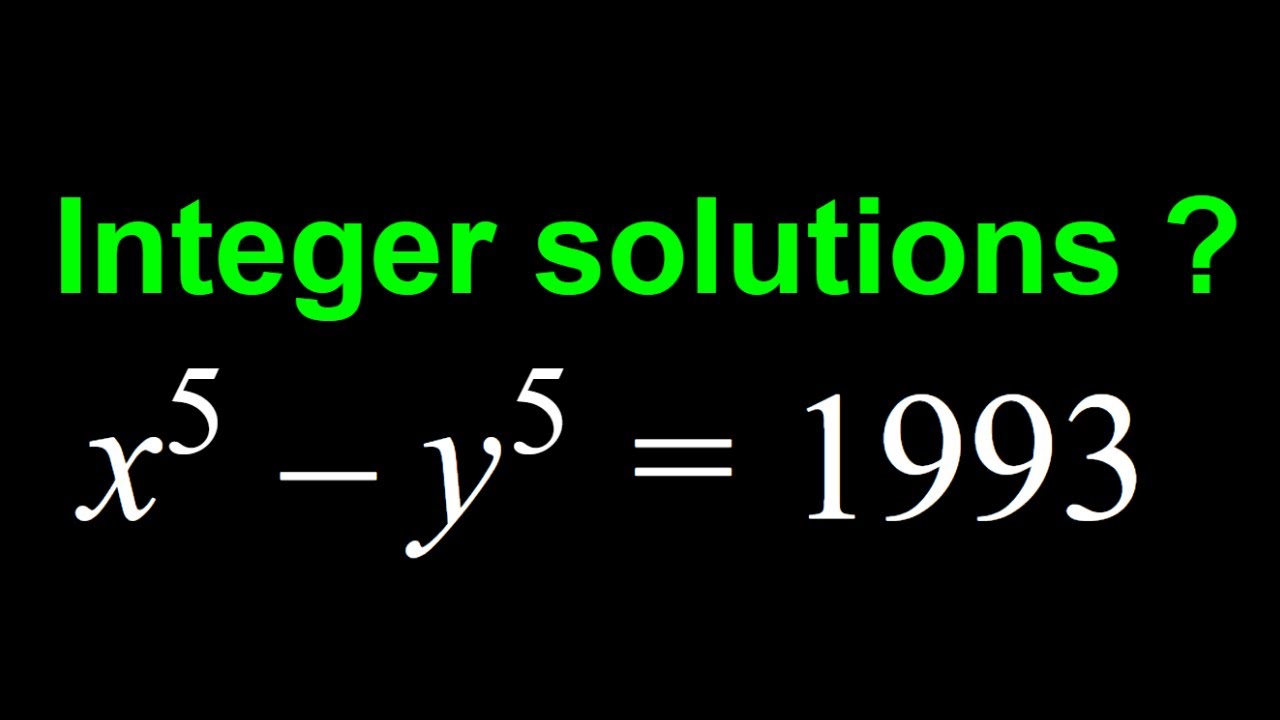
Показать описание
This video is about a Quintic Diophantine Equation
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #DiophantineEquations
EXPLORE:
If you need to post a picture of your solution or idea:
#NumberTheoryProblems #DiophantineEquations
EXPLORE:
A Quintic Diophantine Equation (x^5-y^5=1993)
A Quintic Diophantine Equation | #numbertheory #diophantineequations
Solving 117y^3-x^3=5, a Diophantine Equation
A Linear Diophantine Equation
Solving A Set Of Diophantine Equation In Under A Minute
A Quintic Equation Solved Without The Quintic Formula
Diophantine Equations: Strategies and Examples
Solving a Nice Diophantine Equation in Three Ways
Diophantine Equations with Sum of Squares - mod 4 Analysis
A Linear Diophantine Equation
A Hyperbolic Diophantine Equation
Solving an exponential equation
solving a fractional diophantine equation | Number theory problems
A Quick and Easy Linear Diophantine System
Solving a quintic equation with a non-standard method. An algebraic challenge.
EXPONENTIAL DIOPHANTINE EQUATIONS PART1
Can You Solve a Quintic with Complex Roots? No? Then Watch!
A Nice Diophantine System
Solving a Diophantine System
A Cubic Diophantine Equation: x³ - 6x² + 12x + 27y³ - 224 = 0 || High School Math #FermatLastTheorem...
Solving a cubic system for real solutions
factorization | x5-y5 | mathematics | mathempower | Maths | math trick 31
A Nice Equation with Integer Solutions
Comparing 5^23 and 7^15
Комментарии
 0:15:50
0:15:50
 0:15:50
0:15:50
 0:09:56
0:09:56
 0:00:27
0:00:27
 0:00:58
0:00:58
 0:14:01
0:14:01
 0:27:34
0:27:34
 0:08:13
0:08:13
 0:01:00
0:01:00
 0:10:24
0:10:24
 0:04:52
0:04:52
 0:09:37
0:09:37
 0:03:11
0:03:11
 0:10:57
0:10:57
 0:09:49
0:09:49
 0:06:04
0:06:04
 0:07:19
0:07:19
 0:15:07
0:15:07
 0:07:00
0:07:00
 0:08:29
0:08:29
 0:09:15
0:09:15
 0:05:57
0:05:57
 0:07:34
0:07:34
 0:05:01
0:05:01