filmov
tv
How to find REMOVABLE DISCONTINUITIES (KristaKingMath)

Показать описание
Discontinuities can be characterized as either removable or nonremovable. Removable discontinuities are also called point discontinuities, because they are small holes in the graph of a function at just a single point. They are called removable because they can be "removed" just by redefining the function as the limit of the function at that particular point.
In contrast, nonremovable discontinuities are big breaks in the graph, like asymptotes. They can't just be "filled in" by redefining the function at a point, thereby making it continuous. Therefore, they can't be removed.
You'll usually find removable discontinuities in rational functions, and the removable discontinuity can usually be identified by factoring the numerator and denominator of the function and canceling like factors. It's the solution of these canceled factors that indicate the removable discontinuity.
● ● ● GET EXTRA HELP ● ● ●
● ● ● CONNECT WITH KRISTA ● ● ●
Hi, I’m Krista! I make math courses to keep you from banging your head against the wall. ;)
Math class was always so frustrating for me. I’d go to a class, spend hours on homework, and three days later have an “Ah-ha!” moment about how the problems worked that could have slashed my homework time in half. I’d think, “WHY didn’t my teacher just tell me this in the first place?!”
Комментарии
 0:04:34
0:04:34
 0:08:16
0:08:16
 0:02:16
0:02:16
 0:13:31
0:13:31
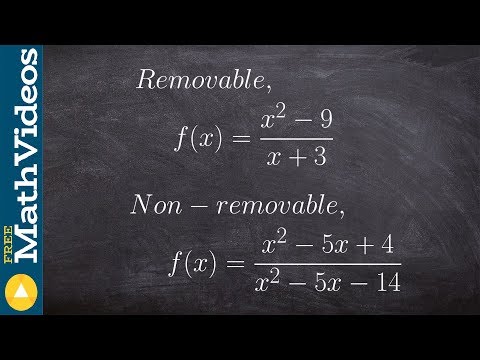 0:02:59
0:02:59
 0:01:02
0:01:02
 0:02:01
0:02:01
 0:01:05
0:01:05
 0:02:48
0:02:48
 0:10:10
0:10:10
 0:06:16
0:06:16
 0:01:50
0:01:50
 0:03:10
0:03:10
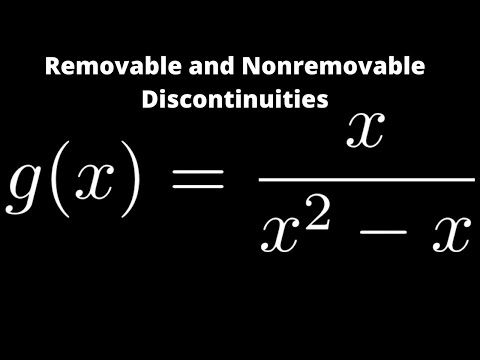 0:01:44
0:01:44
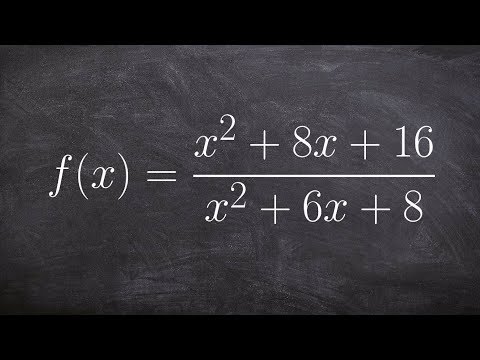 0:01:50
0:01:50
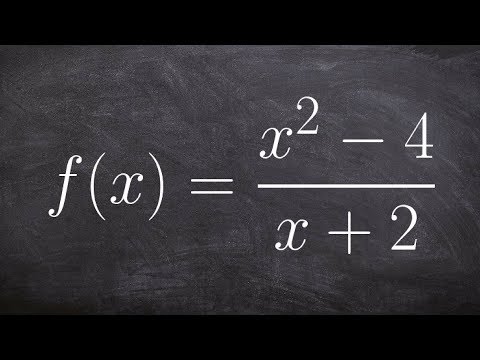 0:01:24
0:01:24
 0:02:07
0:02:07
 0:03:07
0:03:07
 0:05:22
0:05:22
 0:10:07
0:10:07
 0:04:08
0:04:08
 0:04:49
0:04:49
 0:06:37
0:06:37
 0:00:50
0:00:50