filmov
tv
How to find horizontal asymptote, vertical asymptote, & removable discontinuity (calc 1 tutorial)

Показать описание
This calculus tutorial helps you to learn how to find the horizontal asymptote, vertical asymptote, & removable discontinuity. For H.A., we take the limit as x goes to infinity. For V.A. we pay attention to nonzero/0. For R.D. we pay attention to 0/0.
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
Horizontal Asymptote, 0:10
Vertical Asymptote 4:16
Removable Discontinuity 6:47
The graph 10:03
----------------------------------------
#blackpenredpen #math #calculus #apcalculus
Horizontal Asymptote, 0:10
Vertical Asymptote 4:16
Removable Discontinuity 6:47
The graph 10:03
Learn how to find the horizontal asymptote
Horizontal Asymptotes and Slant Asymptotes of Rational Functions
How to Find the Horizontal Asymptote (NancyPi)
Find the vertical and horizontal asymptotes
Rational Graphs Made Easy Find the vertical and horizontal asymptote
Find Horizontal Asymptote of a Rational Function
Identifying vertical, horizontal asymptotes and holes
Quick Trick for Finding Horizontal Asymptotes! PART 1 #math #algebra #mathtrick #mathematics
How to find HORIZONTAL ASYMPTOTES (KristaKingMath)
Determine the horizontal asymptotes
Finding the asymptotes
Finding a Horizontal Asymptote of a Rational Function (Precalculus - College Algebra 40)
What is a horizontal asymptote
Finding the Horizontal Asymptote of an Exponential Function (Example)
❖ Finding Horizontal Asymptotes By Using Limits at Infinity - Another Example #1 ❖
Ex: Determine Horizontal Asymptotes of Rational Functions
How to find the vertical and horizontal asymptotes of a rational function
Limits at Infinity & Horizontal Asymptotes
Determine Horizontal Asymptotes for the Radical Function
#27. Find the Horizontal Asymptote of the Rational Function (Degree in numerator is larger)
9 How To Find Equation of Horizontal Asymptote
Finding the vertical and horizontal asymptotes
Finding horizontal and vertical asymptotes | Rational expressions | Algebra II | Khan Academy
What are Asymptotes? - Nerdstudy
Комментарии
 0:02:36
0:02:36
 0:10:49
0:10:49
 0:04:42
0:04:42
 0:03:54
0:03:54
 0:10:50
0:10:50
 0:02:14
0:02:14
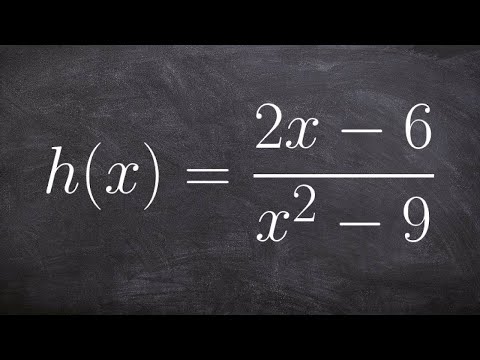 0:02:16
0:02:16
 0:00:57
0:00:57
 0:08:12
0:08:12
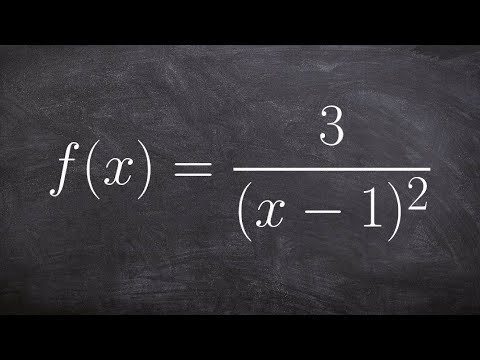 0:04:52
0:04:52
 0:07:08
0:07:08
 0:29:48
0:29:48
 0:03:35
0:03:35
 0:01:54
0:01:54
 0:06:03
0:06:03
 0:05:14
0:05:14
 0:01:59
0:01:59
 0:19:24
0:19:24
 0:08:45
0:08:45
 0:00:58
0:00:58
 0:11:55
0:11:55
 0:02:28
0:02:28
 0:11:22
0:11:22
 0:02:08
0:02:08