filmov
tv
Learn how to identify the discontinuities as removable or non removable
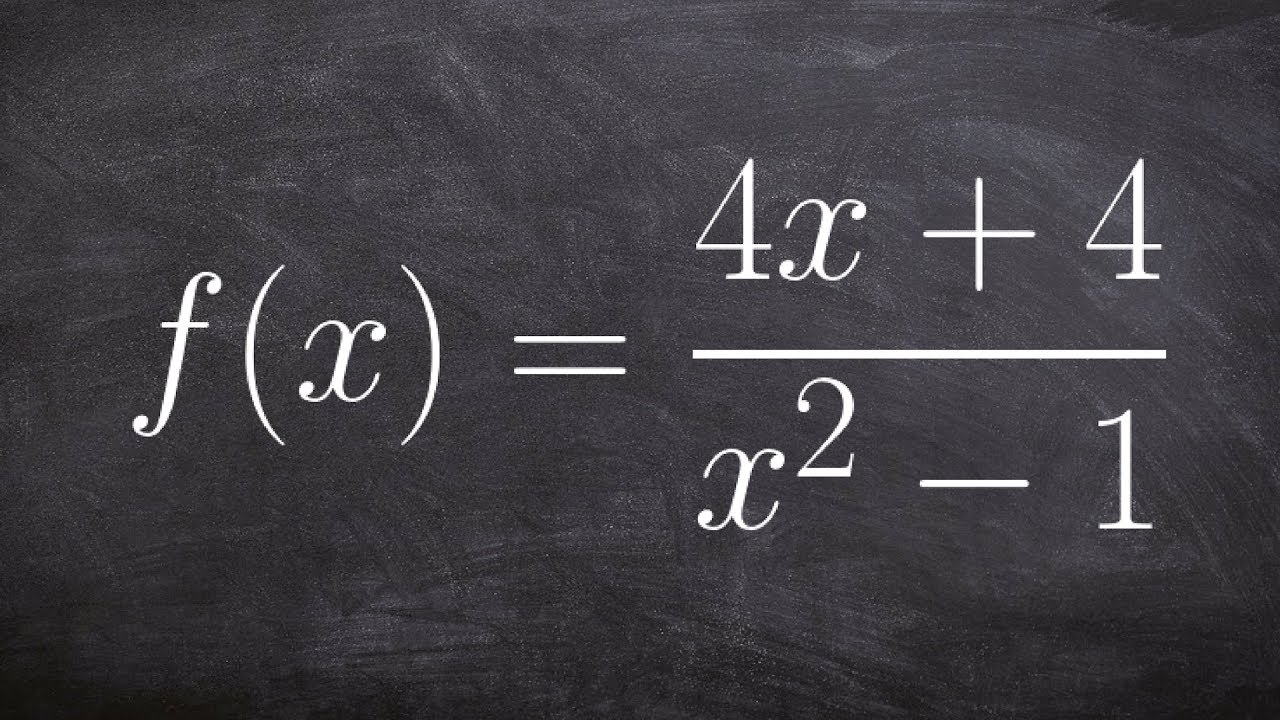
Показать описание
👉 Learn how to find the removable and non-removable discontinuity of a function. A function is said to be discontinuous at a point when there is a gap in the graph of the function at that point. A discontinuity is said to be removable when there is a factor in the numerator which can cancel out the discontinuous factor and is said to be non-removable when there is no factor in the numerator which can cancel out the discontinuous factor.
To find the discontinuities of a rational function, it is usually useful to factor the expressions in the function and we then set the denominator equal to 0 and solve for x. The value of x for which the factor appears in both the numerator and the denominator is the point of removable discontinuity while the value of x for which the factor appears in only the denominator is the point of non-removable discontinuity.
Organized Videos:
✅ Find the Asymptotes of Rational Functions
✅ Find the Vertical and Horizontal Asymptotes of a Rational Function y=0
✅ Asymptotes of Rational Functions | Learn About
✅ Find the Asymptotes of a Rational Function with Trig
✅ Find the Asymptotes and Holes of a Rational Function
✅ Find the Slant Asymptotes of the Rational Function
Connect with me:
#asymptotes #functions #brianmclogan
To find the discontinuities of a rational function, it is usually useful to factor the expressions in the function and we then set the denominator equal to 0 and solve for x. The value of x for which the factor appears in both the numerator and the denominator is the point of removable discontinuity while the value of x for which the factor appears in only the denominator is the point of non-removable discontinuity.
Organized Videos:
✅ Find the Asymptotes of Rational Functions
✅ Find the Vertical and Horizontal Asymptotes of a Rational Function y=0
✅ Asymptotes of Rational Functions | Learn About
✅ Find the Asymptotes of a Rational Function with Trig
✅ Find the Asymptotes and Holes of a Rational Function
✅ Find the Slant Asymptotes of the Rational Function
Connect with me:
#asymptotes #functions #brianmclogan
Комментарии
 0:01:32
0:01:32
 0:06:24
0:06:24
 0:02:16
0:02:16
 0:01:48
0:01:48
 0:13:44
0:13:44
 0:10:13
0:10:13
 0:07:04
0:07:04
 0:11:53
0:11:53
 0:00:54
0:00:54
 0:17:05
0:17:05
 0:12:43
0:12:43
 0:01:06
0:01:06
 0:07:56
0:07:56
 0:03:30
0:03:30
 0:06:43
0:06:43
 0:02:44
0:02:44
 0:05:09
0:05:09
 0:24:07
0:24:07
 0:01:32
0:01:32
 0:03:15
0:03:15
 0:04:17
0:04:17
 0:10:38
0:10:38
 0:00:52
0:00:52
 0:02:01
0:02:01