filmov
tv
Factoring Quadratics... What If You Can't? (NancyPi)
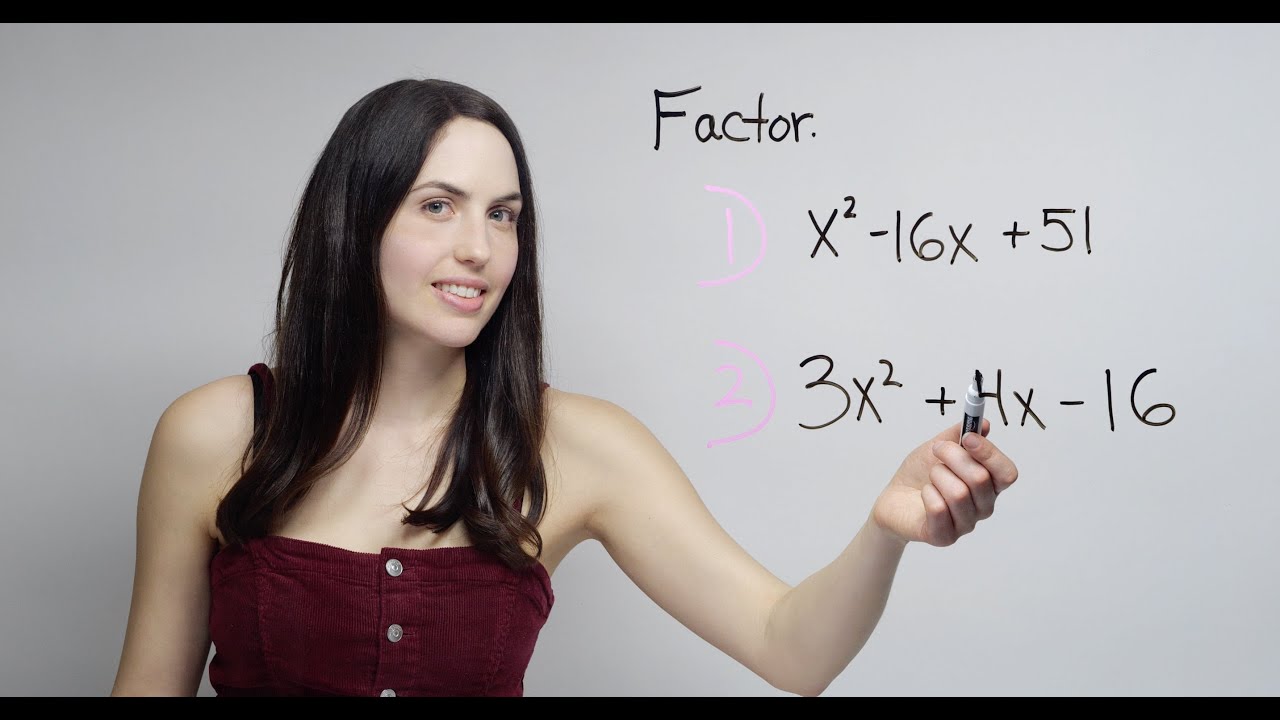
Показать описание
Usually, a quadratic expression can be factored, but some cannot be, at least not with integer numbers. It's best to assume at the beginning that it can be factored, when you're trying to factor the expression. But if you've been working on a problem, and you've already gone through the steps explained in the introduction to factoring video, "Factoring Quadratics...How?", and it's not working, it might be the case that it cannot be factored (using integers).
1) Does the "trial and error" factoring method work for all QUADRATICS STARTING WITH X^2?
For example, say you need to factor the quadratic x^2 - 16x + 51. For the trial and error method, what you need to find are two numbers that multiply to give you the last number, positive 51, and that also add to give you the second number, -16. So first, list all the pairs of numbers that multiply to 51. Then, figure out which of those pairs also adds to negative 16. In this case, none of those pairs of numbers will add to negative 16, so this quadratic cannot be factored (over the integers). It turns out that sometimes the quadratic expression you’re given can't be factored, at least not in the way you're being asked to do in algebra, so you can just write "cannot be factored" as the answer.
2) What about for a quadratic expression that has a LARGER LEADING COEFFICIENT TERM like 2X^2 or 3X^2? Can the "magic X" method be used to factor any quadratic expression?
CAUTION: if your leading coefficient can be factored out from every term, do that. You can pull out that number to the front, as an overall constant, and just use the trial and error method from #1 to factor the remaining x^2 expression (if it can be factored). For example, for 2x^2 + 4x - 14, the leading coefficient 2 can be factored out from every term, so that it becomes 2 (x^2 + 2x - 7).
Say that you're asked to factor the expression 3x^2 + 4x - 16. Since the coefficient 3 can't be factored out from every term, we try to use the magic X method to factor. For the X box you draw on the side, the top number will be the product of the leading coefficient, the first number, times the constant at the end, negative 16. 3 times -16 is negative 48. The bottom number in your X is the second term’s coefficient, positive 4. Then at that point, look for two numbers that multiply to the top number, -48, and add to 4. List out the factors that multiply to -48 and check which ones add to positive 4. Since none of those add to positive 4, in this case the magic X did not help you factor. Why? Because the problem could not be factored.
For those of you who've learned about the discriminant, another way to tell whether a quadratic can be factored is to find the discriminant number, which is D = b^2 - 4ac, where a, b, and c are the coefficients and constant in your quadratic, ax^2 + bx + c. If the D value you calculate is either 0 or a positive perfect square number, then the quadratic expression can be factored.
Again, for factorable problems that CAN be worked out to completion, go to the intro factoring video mentioned above.
Editor: Miriam Nielsen of zentouro @zentouro
Комментарии
 0:05:40
0:05:40
 0:09:14
0:09:14
 0:10:57
0:10:57
 0:04:17
0:04:17
 0:12:29
0:12:29
 0:02:01
0:02:01
 0:02:43
0:02:43
 0:06:24
0:06:24
 0:23:40
0:23:40
 0:05:42
0:05:42
 0:05:53
0:05:53
 0:12:09
0:12:09
 0:03:54
0:03:54
 0:01:00
0:01:00
 0:01:38
0:01:38
 0:04:20
0:04:20
 0:08:52
0:08:52
 0:01:36
0:01:36
 0:08:34
0:08:34
 0:11:54
0:11:54
 0:04:00
0:04:00
 0:00:59
0:00:59
 0:03:50
0:03:50
 0:06:48
0:06:48