filmov
tv
Horizontal Asymptotes and Slant Asymptotes of Rational Functions

Показать описание
This algebra video tutorial explains how to identify the horizontal asymptotes and slant asymptotes of rational functions by comparing the degree of the numerator with the degree of the denominator of the rational expression. The equation of the slant asymptote can be determine using long division if the degree of the numerator exceeds the degree of the denominator by exactly 1. This algebra video tutorial contains plenty of examples and practice problems.
Algebra - Free Formula Sheets:
__________________________________
Fundamental Theorem of Algebra:
Rational Expressions - Basic Intro:
Simplifying Rational Expressions:
Multiplying Rational Expressions:
Dividing Rational Expressions:
______________________________________
Adding & Subtracting Rational Expressions:
Rational Expressions - Unlike Denominators:
Simplifying Complex Rational Expressions:
How To Solve Rational Equations:
Rational Equations - Extraneous Solutions:
_____________________________________
Horizontal and Slant Asymptotes:
Finding Rational Functions Given 2 Points:
Rational Functions - X and Y Intercepts:
Graphing Advanced Rational Functions:
Rational Inequalities:
________________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Algebra - Free Formula Sheets:
__________________________________
Fundamental Theorem of Algebra:
Rational Expressions - Basic Intro:
Simplifying Rational Expressions:
Multiplying Rational Expressions:
Dividing Rational Expressions:
______________________________________
Adding & Subtracting Rational Expressions:
Rational Expressions - Unlike Denominators:
Simplifying Complex Rational Expressions:
How To Solve Rational Equations:
Rational Equations - Extraneous Solutions:
_____________________________________
Horizontal and Slant Asymptotes:
Finding Rational Functions Given 2 Points:
Rational Functions - X and Y Intercepts:
Graphing Advanced Rational Functions:
Rational Inequalities:
________________________________________
Final Exams and Video Playlists:
Full-Length Videos and Worksheets:
Комментарии
 0:10:49
0:10:49
 0:00:57
0:00:57
 0:03:54
0:03:54
 0:00:31
0:00:31
 0:05:25
0:05:25
 0:02:58
0:02:58
 0:00:59
0:00:59
 0:04:42
0:04:42
 0:06:22
0:06:22
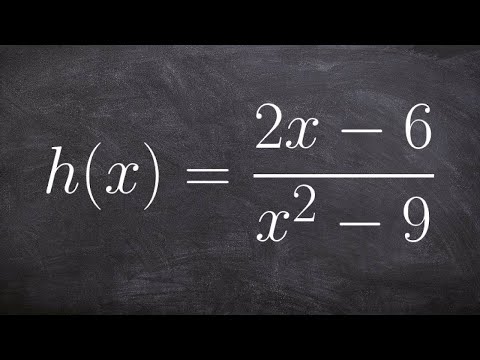 0:02:16
0:02:16
 0:00:59
0:00:59
 0:00:25
0:00:25
 0:00:14
0:00:14
 0:02:21
0:02:21
 0:00:13
0:00:13
 0:02:36
0:02:36
 0:00:36
0:00:36
 0:06:41
0:06:41
 0:00:34
0:00:34
 0:02:08
0:02:08
 0:11:22
0:11:22
 0:03:46
0:03:46
 0:01:00
0:01:00
 0:01:01
0:01:01