filmov
tv
Identifying vertical, horizontal asymptotes and holes
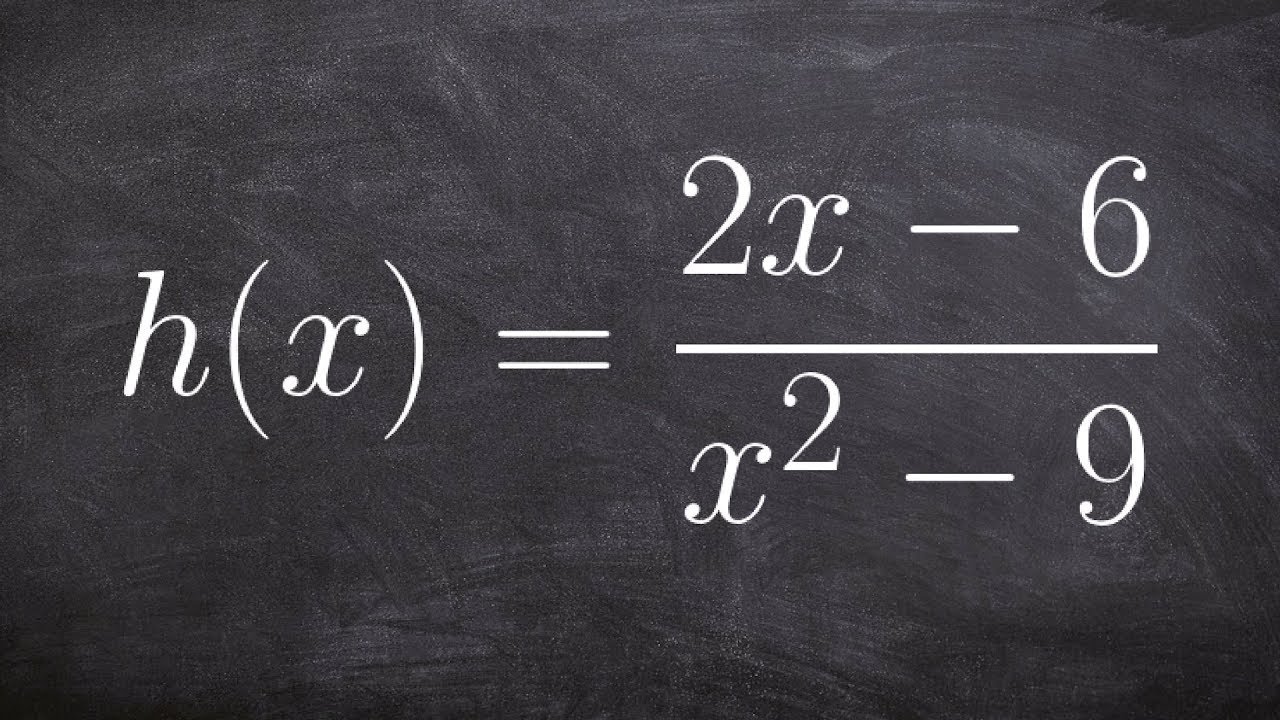
Показать описание
👉 Learn how to find the vertical/horizontal asymptotes of a function. An asymptote is a line that the graph of a function approaches but never touches. The vertical asymptote is a vertical line that the graph of a function approaches but never touches. To find the vertical asymptote(s) of a rational function, we set the denominator equal to 0 and solve for x.
The horizontal asymptote is a horizontal line which the graph of the function approaches but never crosses (though they sometimes cross them). A rational function has a horizontal asymptote of y = 0 when the degree of the numerator is less than the degree of the denominator. A rational function has a horizontal asymptote of y = c, (where c is the quotient of the leading coefficient of the numerator and that of the denominator) when the degree of the numerator is equal to the degree of the denominator. A rational function has no horizontal asymptote if the degree of the numerator is greater than the degree of the denominator.
Organized Videos:
✅ Find the Asymptotes of Rational Functions
✅ Find the Vertical and Horizontal Asymptotes of a Rational Function y=0
✅ Asymptotes of Rational Functions | Learn About
✅ Find the Asymptotes of a Rational Function with Trig
✅ Find the Asymptotes and Holes of a Rational Function
✅ Find the Slant Asymptotes of the Rational Function
Connect with me:
#asymptotes #functions #brianmclogan
The horizontal asymptote is a horizontal line which the graph of the function approaches but never crosses (though they sometimes cross them). A rational function has a horizontal asymptote of y = 0 when the degree of the numerator is less than the degree of the denominator. A rational function has a horizontal asymptote of y = c, (where c is the quotient of the leading coefficient of the numerator and that of the denominator) when the degree of the numerator is equal to the degree of the denominator. A rational function has no horizontal asymptote if the degree of the numerator is greater than the degree of the denominator.
Organized Videos:
✅ Find the Asymptotes of Rational Functions
✅ Find the Vertical and Horizontal Asymptotes of a Rational Function y=0
✅ Asymptotes of Rational Functions | Learn About
✅ Find the Asymptotes of a Rational Function with Trig
✅ Find the Asymptotes and Holes of a Rational Function
✅ Find the Slant Asymptotes of the Rational Function
Connect with me:
#asymptotes #functions #brianmclogan
Комментарии
 0:02:16
0:02:16
 0:03:54
0:03:54
 0:01:50
0:01:50
 0:10:54
0:10:54
 0:02:28
0:02:28
 0:11:22
0:11:22
 0:10:50
0:10:50
 0:10:49
0:10:49
 0:01:52
0:01:52
 0:01:59
0:01:59
 0:07:08
0:07:08
 0:02:53
0:02:53
 0:02:36
0:02:36
 0:06:41
0:06:41
 0:02:37
0:02:37
 0:13:01
0:13:01
 0:02:08
0:02:08
 0:11:30
0:11:30
 0:14:44
0:14:44
 0:04:35
0:04:35
 0:03:55
0:03:55
 0:04:12
0:04:12
 0:00:57
0:00:57
 0:04:53
0:04:53