filmov
tv
How to Find the Horizontal Asymptote (NancyPi)
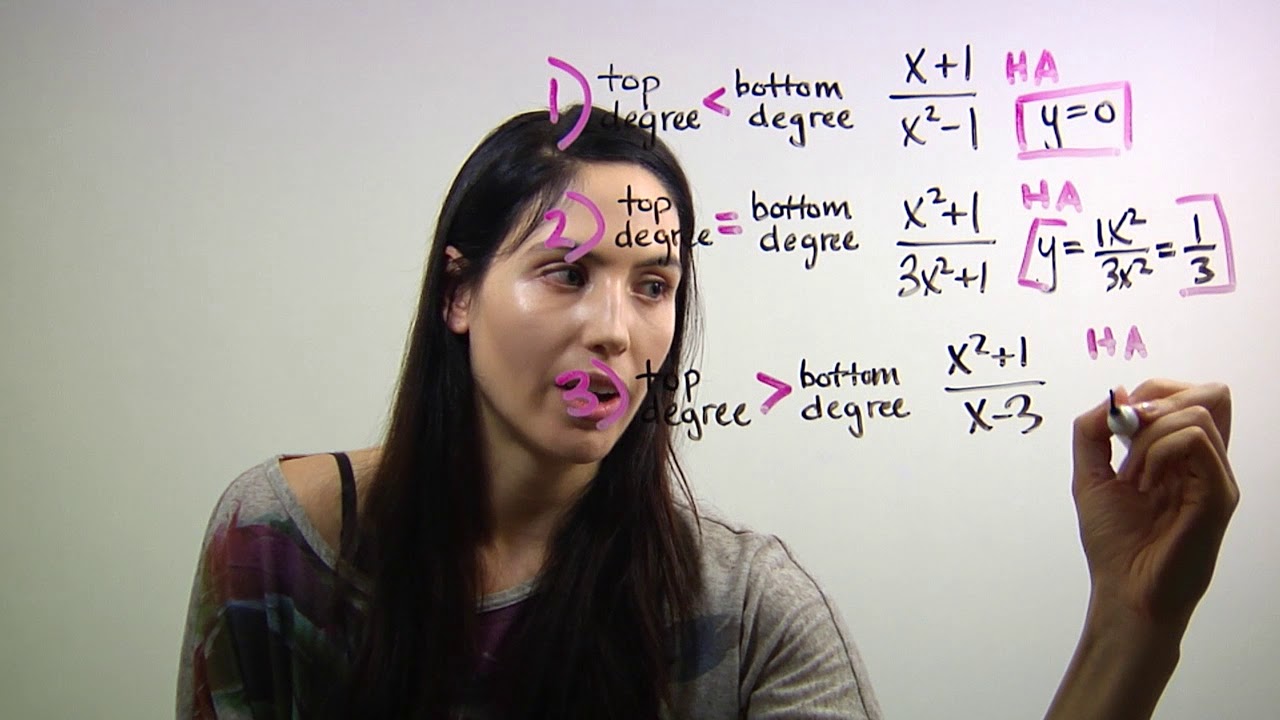
Показать описание
MIT grad shows how to find the horizontal asymptote (of a rational function) with a quick and easy rule. Nancy formerly of MathBFF explains the steps.
The degree of a function is the highest power of x that appears in the polynomial. To find the horizontal asymptote, there are three easy cases. 1) If the degree of the numerator expression is less than the degree of the denominator expression, then the horizontal asymptote is y=0 (the x-axis). 2) If the degree of the numerator is equal to the degree of the denominator, then you can find the horizontal asymptote by dividing the first, highest term of the numerator by the first, highest term of the denominator. This will simplify to y = some constant (just a number). 3) If the degree of the numerator is greater than the degree of the denominator, then there is no horizontal asymptote.
The degree of a function is the highest power of x that appears in the polynomial. To find the horizontal asymptote, there are three easy cases. 1) If the degree of the numerator expression is less than the degree of the denominator expression, then the horizontal asymptote is y=0 (the x-axis). 2) If the degree of the numerator is equal to the degree of the denominator, then you can find the horizontal asymptote by dividing the first, highest term of the numerator by the first, highest term of the denominator. This will simplify to y = some constant (just a number). 3) If the degree of the numerator is greater than the degree of the denominator, then there is no horizontal asymptote.
 0:02:36
0:02:36
 0:04:42
0:04:42
 0:03:54
0:03:54
 0:01:56
0:01:56
 0:08:12
0:08:12
 0:10:49
0:10:49
 0:08:06
0:08:06
 0:01:00
0:01:00
 0:12:17
0:12:17
 0:06:41
0:06:41
 0:02:16
0:02:16
 0:01:59
0:01:59
 0:02:28
0:02:28
 0:09:14
0:09:14
 0:10:50
0:10:50
 0:00:58
0:00:58
 0:11:22
0:11:22
 0:02:53
0:02:53
 0:01:54
0:01:54
 0:02:14
0:02:14
 0:06:22
0:06:22
 0:04:52
0:04:52
 0:03:47
0:03:47
 0:04:09
0:04:09