filmov
tv
A second proof of 1=2

Показать описание
Mr. John Hush presents a second proof of 1=2 for those who doubted the first one. He noticed that a couple viewers proposed this one so he wishes to share it with everyone. What's wrong with this proof, if anything?!
The 360-Page Proof That 1+1=2
Proof that 1 = 2.
1=2 Proof
(ASMR) PROOF that 1 = 2 #Shorts
Proof that 1+1 = 2 【Fundamentals of Mathematics】
The 379 page proof that 1+1=2
ASTOUNDING: 1 + 2 + 3 + 4 + 5 + ... = -1/12
'Prove' 2 = 1 Using Calculus Derivatives - Can You Spot The Mistake?
TNPSC GROUP 1,2,2A, 4,VAO - TEST SERIES - 30 TEST - 300 RS - 9600819370
The paradox at the heart of mathematics: Gödel's Incompleteness Theorem - Marcus du Sautoy
Numberphile v. Math: the truth about 1+2+3+...=-1/12
Why is pi here? And why is it squared? A geometric answer to the Basel problem
Math's Fundamental Flaw
Induction Proof for Sum of First n Powers of 2 (2^0 + 2^1 + ... + 2^n = 2^(n+1) - 1)
Every Student Should See This
Math Prof answers 6÷2(1+2) = ? once and for all ***Viral Math Problem***
The Most Classic Proof By Induction
A Proof That The Square Root of Two Is Irrational
1 + 1 = 3 Proof | Breaking the rules of mathematics
Why was this visual proof missed for 400 years? (Fermat's two square theorem)
Proof by Mathematical Induction - How to do a Mathematical Induction Proof ( Example 1 )
Mathematical Induction Practice Problems
Sum of Natural Numbers (second proof and extra footage)
The Simplest Math Problem No One Can Solve - Collatz Conjecture
Комментарии
 0:06:03
0:06:03
 0:02:59
0:02:59
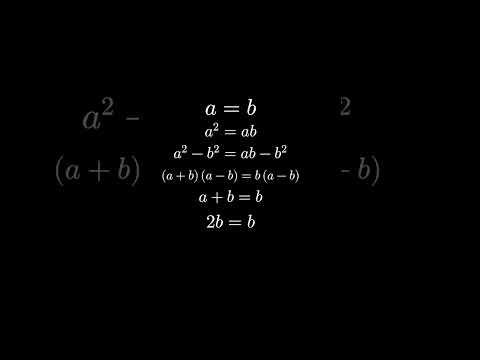 0:00:58
0:00:58
 0:00:59
0:00:59
 0:12:16
0:12:16
 0:16:43
0:16:43
 0:07:50
0:07:50
 0:04:21
0:04:21
 0:04:03
0:04:03
 0:05:20
0:05:20
 0:41:44
0:41:44
 0:17:08
0:17:08
 0:34:00
0:34:00
 0:08:27
0:08:27
 0:00:58
0:00:58
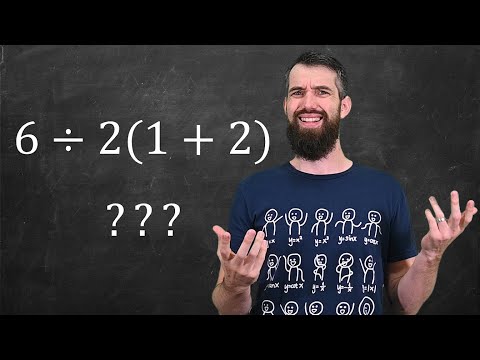 0:06:04
0:06:04
 0:00:40
0:00:40
 0:17:22
0:17:22
 0:08:25
0:08:25
 0:33:59
0:33:59
 0:07:32
0:07:32
 0:18:08
0:18:08
 0:21:06
0:21:06
 0:22:09
0:22:09