filmov
tv
Given Vertex of Quadratic Equation Find the Sum of b and c

Показать описание
Standard Form to Vertex Form - Quadratic Equations
Finding the vertex of a quadratic function
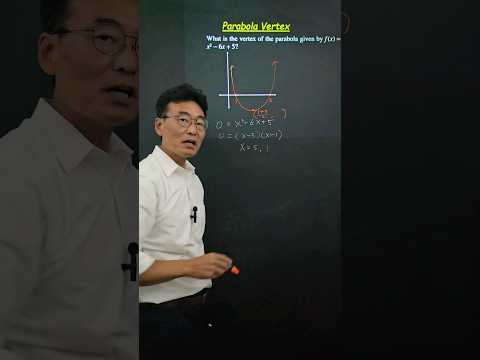
Vertex of Parabola Using X-Intercepts
Finding the vertex of a parabola example | Quadratic equations | Algebra I | Khan Academy
Finding the Vertex Of Parabola
Determining the quadratic equation given a vertex and a point
Given Vertex of Quadratic Equation Find the Sum of b and c
Vertex of a Parabola (SAT Math Formula 13/23)
Centroid of Parabola
How to Find the Vertex of Parabola - Quadratic Function y = ax² + bx + c
Standard to Vertex form - Quadratic Equations
Find Missing Term in Quadratic Equation for Given Vertex
Find the Vertex of the Quadratic in Standard Form (y=ax²+bx+c)
How do you Find the Quadratic Equation from Given Vertex
Parabola Concave Up Shift Up | Sketching Quadratic Graphs
Given the vertex and focus learn to write the equation of the parabola in standard form
Graphing Parabolas in Vertex Form
Find a,b,c Given Vertex is (1,4) And Passes through (-1,-8). Quadratic Function
Find the axis of symmetry and your vertex
Finding the standard form of a parabola given vertex and focus
Graphing a parabola in vertex form | Quadratic equations | Algebra I | Khan Academy
How to Find the Vertex of a Parabola (NancyPi)
Ex: Find a Quadratic Function Given the Vertex and the Leading Coefficient
Write the equation of a parabola given vertex, axis of symmetry & point it passes through
Комментарии
 0:02:43
0:02:43
 0:03:30
0:03:30
 0:01:01
0:01:01
 0:05:40
0:05:40
 0:00:56
0:00:56
 0:05:28
0:05:28
 0:04:58
0:04:58
 0:00:19
0:00:19
 0:00:35
0:00:35
 0:04:30
0:04:30
 0:05:46
0:05:46
 0:02:12
0:02:12
 0:00:49
0:00:49
 0:13:51
0:13:51
 0:00:25
0:00:25
 0:04:51
0:04:51
 0:02:44
0:02:44
 0:03:40
0:03:40
 0:04:49
0:04:49
 0:05:26
0:05:26
 0:03:16
0:03:16
 0:05:05
0:05:05
 0:03:19
0:03:19
 0:03:36
0:03:36