filmov
tv
Finding the standard form of a parabola given vertex and focus

Показать описание
Learn how to write the equation of a parabola given the vertex and the focus. A parabola is the shape of the graph of a quadratic equation. A parabola can open up or down (if x is squared) or open left or right (if y is squared). Recall that the focus and the vertex of a parabola are on the same line of symmetry.
When given the focus and the vertex of a parabola, recall that the focus of a parabola is inside the parabola. This enables us to identify the direction which the required parabola opens. We also need to identify the value of p, which is the distance between the vertex and the focus. p is negative when the parabola opens down or left and is positive when the parabola opens right or up.
Once we identify the direction and the value of p, we can use the equation of parabola given by (y - k)^2 = 4p(x - h) for parabolas that opens up or down and (x - h)^2 = 4p(y - k) for parabolas that opens left or right
#conicsections #parabolaconicsections
When given the focus and the vertex of a parabola, recall that the focus of a parabola is inside the parabola. This enables us to identify the direction which the required parabola opens. We also need to identify the value of p, which is the distance between the vertex and the focus. p is negative when the parabola opens down or left and is positive when the parabola opens right or up.
Once we identify the direction and the value of p, we can use the equation of parabola given by (y - k)^2 = 4p(x - h) for parabolas that opens up or down and (x - h)^2 = 4p(y - k) for parabolas that opens left or right
#conicsections #parabolaconicsections
The Maths Prof: Standard Form (part 1)
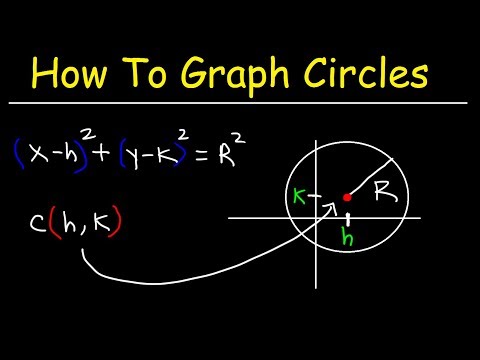
How to find the center and radius of a circle in standard form
Standard Form to Vertex Form - Quadratic Equations
How to write a linear equation in standard form
How to Write a Line in Standard Form
How To Convert From Slope Intercept Form to Standard Form | Algebra
Finding the standard form of a parabola given vertex and focus
Completing the square to write equation in standard form of a circle | Algebra II | Khan Academy
How do I set up custom email notifications for Security Hub findings with EventBridge and SNS?
Circle: Transforming General Equation to Standard Form and Graph | Grade10 Math| Part 1
Graphing Circles and Writing Equations of Circles In Standard Form - Conic Sections
What is standard form of a quadratic equation
How to Convert Number into Standard Form (Part 2/4) #24
Express each of the following rational number in standard form
Center Radius Form to General Form of the Equation of Circle - Grade 10 Math
Graphing Equations in Standard Form
Finding Standard Form of Equation - Second Grade Math (2.NBT.1.S5)
Write Standard Form (when given two points)
Finding the vertex from a quadratic equation by using the standard form
Ex: Write the Standard Form of a Circle From a Graph
Parabolas: Finding the vertex in standard form, vertex form, and intercept form
How to write a polynomial in standard form
Finding the Equation of a Line in Standard Form
Find the center and radius of a circle in standard form
Комментарии
 0:04:52
0:04:52
 0:05:06
0:05:06
 0:02:43
0:02:43
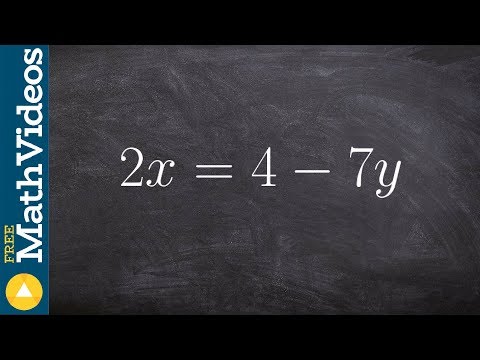 0:02:19
0:02:19
 0:04:30
0:04:30
 0:12:09
0:12:09
 0:05:26
0:05:26
 0:04:20
0:04:20
 0:03:45
0:03:45
 0:13:39
0:13:39
 0:10:04
0:10:04
 0:01:54
0:01:54
 0:04:26
0:04:26
 0:02:16
0:02:16
 0:10:19
0:10:19
 0:04:47
0:04:47
 0:01:03
0:01:03
 0:02:41
0:02:41
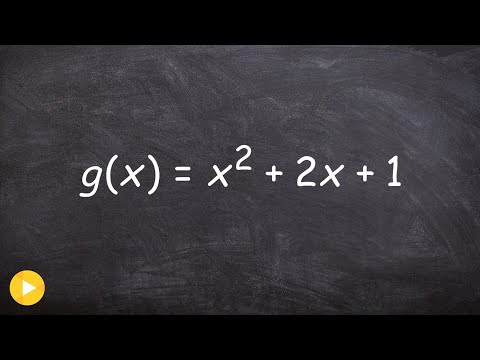 0:01:57
0:01:57
 0:01:39
0:01:39
 0:05:41
0:05:41
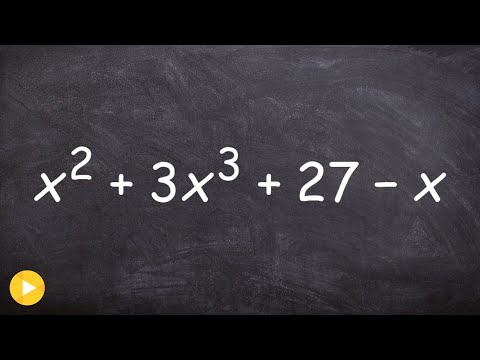 0:02:41
0:02:41
 0:03:47
0:03:47
 0:02:02
0:02:02