Limit of |x|/x as x approaches 0 Does Not Exist | Calculus 1

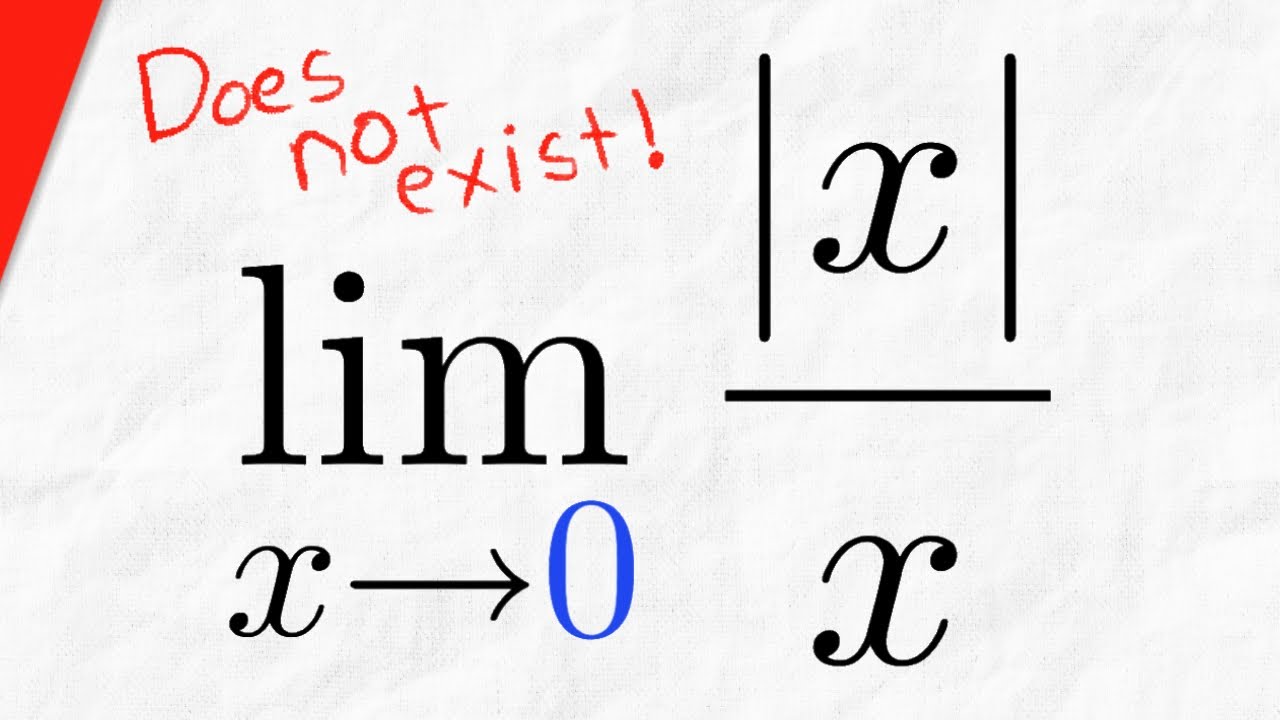
preview_player
Показать описание
We show the limit of absolute value of x over x, as x goes to zero, does not exist. This is because as x approaches 0 from the left, it is negative, so |x| = -x, and then |x|/x = -x/x = -1. However, as x approaches 0 from the right, it is positive, so |x|/x = x/x = 1. Thus, the one sided limits are different and so the two sided limit does not exist. #Calculus1

◉Textbooks I Like◉

★DONATE★

Thanks to Petar, dric, Rolf Waefler, Robert Rennie, Barbara Sharrock, Joshua Gray, Karl Kristiansen, Katy, Mohamad Nossier, and Shadow Master for their generous support on Patreon!

Follow Wrath of Math on...

  1. Wrath of Math
  2. wrath of math
  3. math lessons
  4. math
  5. education
  6. math video
Рекомендации по теме
Limit of x! 0:10:49

Limit of x! over x^x as x goes to infinity

Limit of x^x 0:08:28

Limit of x^x as x goes to 0+

Limit as X 0:06:28

Limit as X approaches 0 from the right of X^X

Limit of x/(x^2 0:01:49

Limit of x/(x^2 + 7x) as x approaches 0

Deriving e from 0:06:33

Deriving e from the limit (1+1/x)^x as x approaches infinity

Limit of sin(x)/x 0:03:59

Limit of sin(x)/x as x goes to Infinity (Squeeze Theorem) | Calculus 1 Exercises

How To Find 0:13:14

How To Find The Limit At Infinity

Limit of sin(x)/x 0:09:16

Limit of sin(x)/x as x approaches 0 | Derivative rules | AP Calculus AB | Khan Academy

Prove using epsilon-delta: 0:11:11

Prove using epsilon-delta: Limit of (2x^2 - 3x + 1)/(x^3 + 4) = 1/4 as x approaches 2

Limit of the 0:08:58

Limit of the xth root of x as x approaches infinity

Limit of lnx/x 0:02:21

Limit of lnx/x as x goes to Infinity (L'Hospital's Rule) | Calculus 1 Exercises

limit of x*tan(1/x) 0:03:36

limit of x*tan(1/x) as x goes to infinity, L'Hospital's Rule

Limit of (1-cos(x))/x 0:04:05

Limit of (1-cos(x))/x as x approaches 0 | Derivative rules | AP Calculus AB | Khan Academy

The Limit (do 0:12:08

The Limit (do not use L'Hospital rule)

L'Hospital's Rule Twice! 0:05:56

L'Hospital's Rule Twice! Limit of e^x / x^2 as x approaches Infinity | Calculus I Exercis...

The most important 0:11:54

The most important limit in Calculus // Geometric Proof & Applications

Limits at Infinity 0:19:24

Limits at Infinity & Horizontal Asymptotes

Calculus 6.08k - 0:06:16

Calculus 6.08k - Limit of 1+1 over x to the x

Evaluate the limit 0:05:00

Evaluate the limit as x approaches infinity of (e^x + x)^(1/x). l’Hopital’s Rule

Learn how to 0:01:40

Learn how to evaluate a limit at infinity

Proof: Limit of 0:10:21

Proof: Limit of sinx/x as x approaches 0 with Squeeze Theorem | Calculus 1

Limit of tanx/x 0:03:22

Limit of tanx/x as x approaches 0 | Calculus 1 Exercises

Limit of lnx 0:03:36

Limit of lnx as x approaches 0 | Real Analysis Exercises

Calculus Limits at 0:03:52

Calculus Limits at Infinity The Limit of x/sqrt(x^2 - x) as x approaches negative infinity

Комментарии
Автор

Currently studying for JEE exam and got stuck on 1st question of limits 😅. Thanks for explaining though

tadipaar
Автор

This question appeared in a list of exercises for Calculus 1 and I didn't understand why the answer was 1 and -1 and just seeing the first explanation of 0-, I understood why. Thank you very much!!!!

rosanepaula
Автор

You are an excellent teacher Mr. Wrathy! 👏

arjunob
Автор

could you do a proof for this same problem?

daliobenavidez
Автор

Hello, can I please ask you a question on subsets? how many subsets of {1, 2, 3, …, 20} are there with no more than 2 consecutive integers? Can you please explain step by step how to arrive at the answer?

zacksnyder
Автор

I am new to this subject please help me : when x reaches from the left side (negative) the absolute value of it or mod will positive x then why is it -x

codewithdevhindi
Автор

More context: This is the derivative of the absolute value function which has a sharp corner at the origin.

Abs(x)=sqrt(x^2), chain rule leads to your result.

You must of had your coffee before the video today 😊

MyOneFiftiethOfADollar