filmov
tv
Limit of x! over x^x as x goes to infinity

Показать описание
Limit of x!/x^x as x goes to infinity using the squeeze theorem.
A superb limit problem: lim {x \to 0} (x!)^(1/x)
Limit of x^x as x goes to 0+
Limit as X approaches 0 from the right of X^X
Limit of x/(x^2 + 7x) as x approaches 0
How To Find The Limit At Infinity
Limit of sin(x)/x as x goes to Infinity (Squeeze Theorem) | Calculus 1 Exercises
Learn how to evaluate a limit at infinity
Limit of the xth root of x as x approaches infinity
Limit and Infinity (calculus basics)
The Limit (do not use L'Hospital rule)
limit of x-root of x, calculus 1 tutorial
Calculus 6.08k - Limit of 1+1 over x to the x
Evaluate the limit of sinx over x
Deriving e from the limit (1+1/x)^x as x approaches infinity
The most important limit in Calculus // Geometric Proof & Applications
Limit of sin(x)/x as x approaches 0 | Derivative rules | AP Calculus AB | Khan Academy
limit of x*tan(1/x) as x goes to infinity, L'Hospital's Rule
Limit of sqrt(9x^6 - x)/(x^3 + 1) as x approaches infinity
How to Find Any Limit (NancyPi)
Limit of lnx/x as x goes to Infinity (L'Hospital's Rule) | Calculus 1 Exercises
Learn how to evaluate the limit at infinity of a trigonometric function
Find the Limit of (2 - x)/(x - 1)^2 as x approaches 1
Calculus Limits at Infinity The Limit of x/sqrt(x^2 - x) as x approaches negative infinity
Limit of (1-cos(x))/x as x approaches 0 | Derivative rules | AP Calculus AB | Khan Academy
Комментарии
 0:08:19
0:08:19
 0:08:28
0:08:28
 0:06:28
0:06:28
 0:01:49
0:01:49
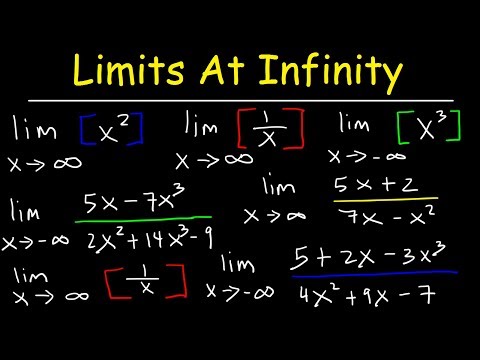 0:13:14
0:13:14
 0:03:59
0:03:59
 0:01:40
0:01:40
 0:08:58
0:08:58
 0:00:55
0:00:55
 0:12:08
0:12:08
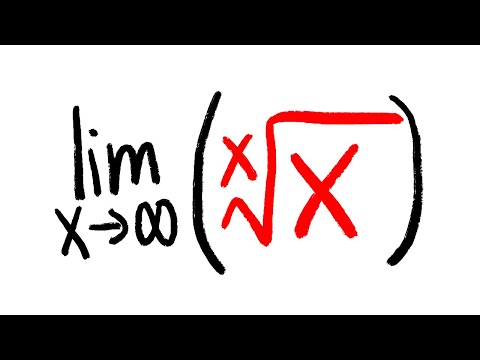 0:04:11
0:04:11
 0:06:16
0:06:16
 0:03:28
0:03:28
 0:06:33
0:06:33
 0:11:54
0:11:54
 0:09:16
0:09:16
 0:03:36
0:03:36
 0:03:42
0:03:42
 0:16:42
0:16:42
 0:02:21
0:02:21
 0:03:20
0:03:20
 0:02:18
0:02:18
 0:03:52
0:03:52
 0:04:05
0:04:05