filmov
tv
Limit as X approaches 0 from the right of X^X

Показать описание
🙏Support me by becoming a channel member!
#math #brithemathguy
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information. Viewers should always verify the information provided in this video by consulting other reliable sources.
#math #brithemathguy
Disclaimer: This video is for entertainment purposes only and should not be considered academic. Though all information is provided in good faith, no warranty of any kind, expressed or implied, is made with regards to the accuracy, validity, reliability, consistency, adequacy, or completeness of this information. Viewers should always verify the information provided in this video by consulting other reliable sources.
Limit of x/(x^2 + 7x) as x approaches 0
How to Find Any Limit (NancyPi)
Limit as X approaches 0 from the right of X^X
Infinite Limits and Vertical Asymptotes
Limits of Trigonometric Functions
How To Find The Limit At Infinity
Limit of sin(x)/x as x approaches 0 | Derivative rules | AP Calculus AB | Khan Academy
A superb limit problem: lim {x \to 0} (x!)^(1/x)
Dr. C's Calc101 Limits Quiz #calculus #maths #Limits #viral math videos
Calculus 1 - Introduction to Limits
Limit of (1-cos(x))/x as x approaches 0 | Derivative rules | AP Calculus AB | Khan Academy
Limit of |x|/x as x approaches 0 Does Not Exist | Calculus 1
Limit of sin^8(x)/x as x approaches 0
Evaluate the limit as x approaches 0 for sin(5x)/x. l’Hopital’s Rule
Limit of x^x as x approaches 0 | Calculus 1 Exercises
Find the limit as x approaches 0^+ for x^(sqrt(x)) l’Hopital’s Rule
Evaluating Limits By Factoring
Limit of sin(x)/(5x) as x approaches 0
Find the limit as x approaches 0^+ of (1 + 1/x)^x. l’Hopital’s Rule
Epsilon M Definition of a Limit as x Approaches 0
Find the limit as x approaches 0 for (1- 2x)^(1/x). l’Hopital’s Rule
Limits of Rational Functions - Fractions and Square Roots
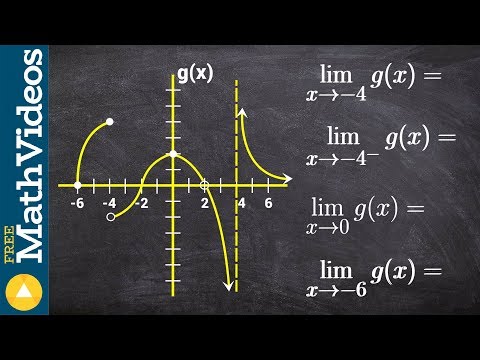
Evaluate all the limits from a given graph
Squeeze Theorem
Комментарии
 0:01:49
0:01:49
 0:16:42
0:16:42
 0:06:28
0:06:28
 0:29:04
0:29:04
 0:15:23
0:15:23
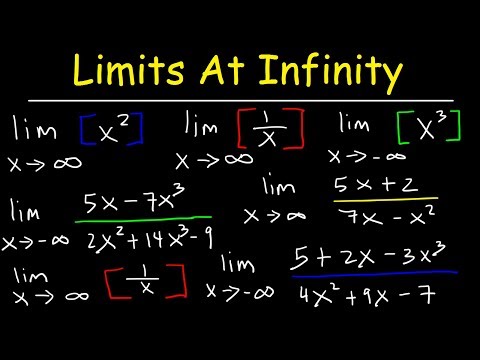 0:13:14
0:13:14
 0:09:16
0:09:16
 0:08:19
0:08:19
 0:01:00
0:01:00
 0:20:20
0:20:20
 0:04:05
0:04:05
 0:05:03
0:05:03
 0:02:40
0:02:40
 0:02:37
0:02:37
 0:05:30
0:05:30
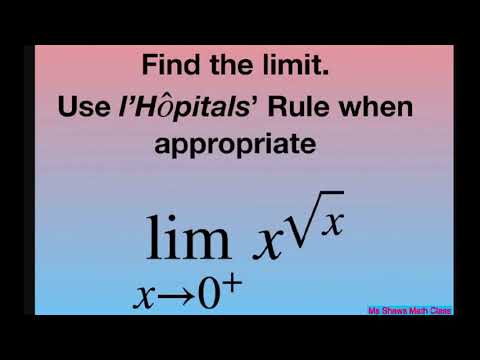 0:05:32
0:05:32
 0:11:35
0:11:35
 0:01:18
0:01:18
 0:05:09
0:05:09
 0:03:21
0:03:21
 0:04:16
0:04:16
 0:10:06
0:10:06
 0:05:34
0:05:34
 0:10:43
0:10:43