Golden ratio!

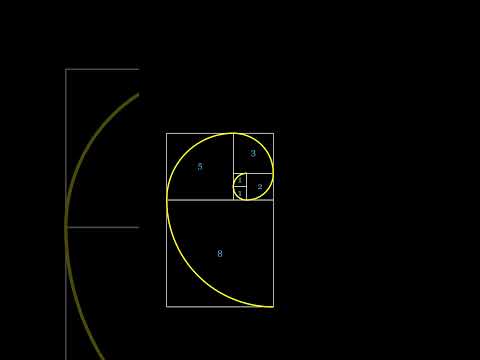
This is a short, animated visual proof of showing how to compute the value of the golden ratio (which is the positive number satisfying x=1+1/x) without using the quadratic formula explicitly. Instead, we use a Tatami diagram and compute the areas of the included rectangles and squares to find the total area of the outer square in two ways.

Check out these related videos:

If you like this video, please click "like" and consider subscribing and checking out my other videos.

#manim #math #mathvideo #goldenratio #goldensection #mathshorts #geometry #animation #theorem #pww #proofwithoutwords #visualproof #proof #area #algebra #pww​​ ​ #proof​ #areas #mathematics​​ #mtbos

To learn more about animating with manim, check out:

[cheeseheadfiddle]

I’m a golden ratio nerd. But I’d never seen this before. So brilliant.

[bunleap]

Gyro be making a power poin presentation for johnny be like:

[lgooch]

Another nice appearance of the golden ratio in geometry is that the ratio of the diagonal of a regular pentagon to its side length is the golden ratio. This can be proved with ptolemys theorem or basic trigonometry.

[ultimatememe]

You can also just multiply both sides by x at the beginning and rearrange the values to get x² - x - 1 = 0, which is a simple quadratic. Then you can plug it into the quadratic equation to see that x = (1 + or - sqrt(5))/2, and since x > 0, you know that x must be the golden ratio.

I love the visual explanation of it though!

[MichaelRothwell]

Beautiful proof!

Here is my interpretation of this visual proof as a visual way of completing the square (but here I use x-1 instead of 1/x).

(Please see my reply starting "P.S." below to see how a version of this visual proof can be applied to practically any monic quadratic with a positive root).

x²-x-1=0, x>0
x²-x=1
x(x-1)=1 (area of one rectangle, says x-1=1/x)
We need to add ¼ to each side to complete the square.
But, to avoid fractions, let's multiply both sides by 4
4x(x-1)=4 (area of four rectangles)
Now we just need to add 1 to each side to complete the square.
4x(x-1)+1=4+1 (area of four rectangles plus unit square)
A bit of algebra and...
(2x-1)²=5 (area of the large square)
2x-1=√5
2x=√5+1
x=(1+√5)/2.

[anjalidwivedi]

It was all so smooth and suddenly you put in the golden ratio...and now it's more smooth.. 😀😀

[That_dude_]

We finding the Corpse parts with this one🗣️🔥🗣️

[phi]

I love the golden ratio, it is for it that I chose my name.

[krishpandey]

How do people figure this stuff out. Like, how tf did someone see a square from that equation.

[peternotpan]

Can you explain this?
I don’t get when you subtract 1/x from x and it becomes 1!

[abubakargabol]

You are doing great work but also explain your videos with your voice in background instead of music

[sci-simply]

We can find these metallic ratios simply by using the formula

N+√N²+1 / 2


Puting n = 0, we get platinum ratio which is 0

Puting n = 1, we get golden ratio which is 1+√5/2

Puting n=2, we get silver ratio which is

[kishlaykumar]

While studying trigonometry I realised 2cos36 = golden ratio 🗿

[poop_eater]

Honestly, I find it much easier to use the quadratic equation to solve this

[themak]

You lost me on how you got 1 from x-1/x

[neologicalgamer]

That's actually cool as shit. How would you fit in it's negative counterpart?

[goldenboy]

I think you can also solve it by the discriminate

[srimanjunathan]

While looking at thumbnail I thought it was A Golden Harvest Presentation. 😀

[herobrineog]

Omg is this a reference to the former top 1 level in the hit game geometry dash, by Robtop, named The Golden by

[tazguy]

Kill the music and say what you’re doing