filmov
tv
Proof that if g o f is Injective(one-to-one) then f is Injective(one-to-one)
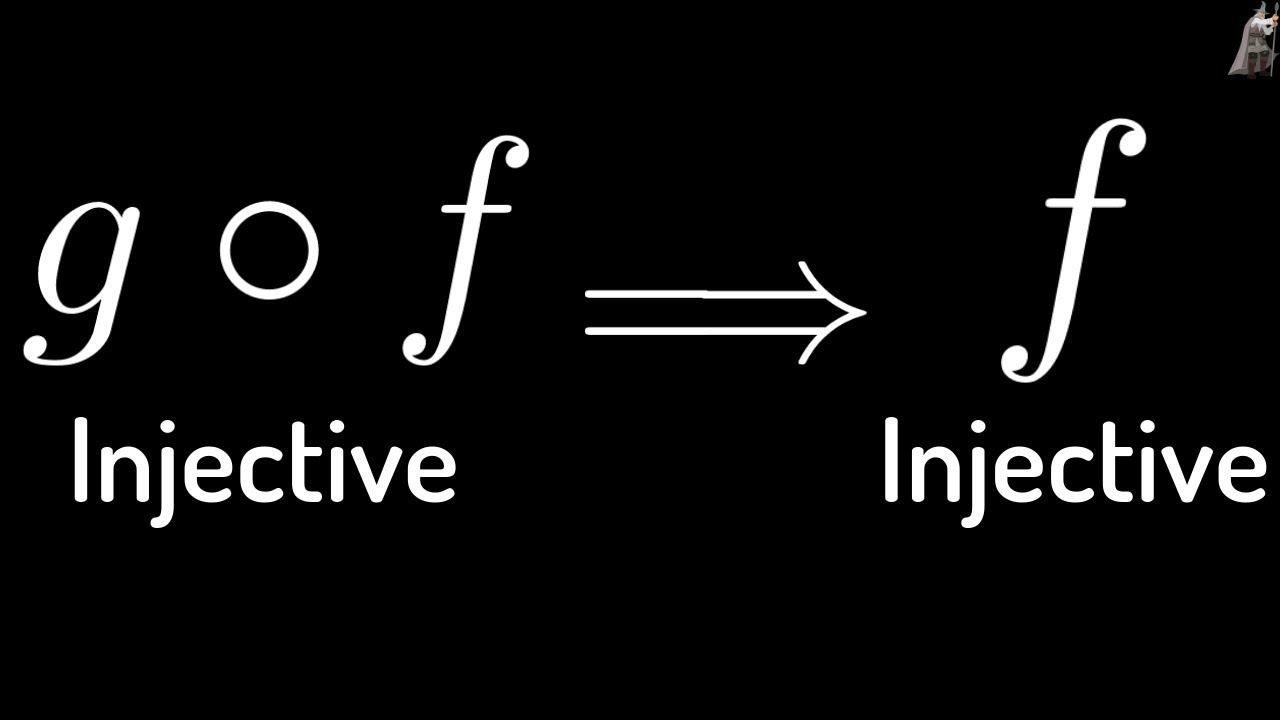
Показать описание
Proof that if g o f is Injective(one-to-one) then f is Injective(one-to-one). Given two functions f : A to B and g: B to C, we prove that if the composition g o f: A to C is an injective function then f is also an injective function.
Proof that if g o f is Surjective(Onto) then g is Surjective(Onto)
Group Theory Proof: If g^n = e then the order of g divides n
Proof that o(x) divides |G| if G is Finite
Islands On Earth If You Go To, You Will Die! #Shorts
How Deep Into The Earth Will This Go from 1000ft?
Abstract Algebra | If G/Z(G) is cyclic then G is abelian.
Proof that f(a) = a^(-1) is a Group Isomorphism if G is Abelian
Westlife - If I Let You Go (Lyrics)
Let’s see if the ball can go viral #ball # go viral
If G is a group, then (a^-1)^-1=a for all a in G.
If I Go, I'm Goin' (The Haunting of Hill House Version)
If x^2 = e for all x in G then G is an abelian group proof
If G is Cyclic so is G/H Proof
18. If G is a group and it has only element 'a' whose order is 2 then ax=xa
If I go down, we go down together 🥰 @asherlara #sofimanassyan #relatable #friends
Angie Martinez ft. Lil' Mo & Sacario – If I Could Go! (Official Video)
Blakey - If I Go (Lyrics)
If I Go, I'm Goin - Gregory Alan Isakov with Aoife O'Donovan & Chris Thile | Live from...
What If The Titanoboa Didn't Go Extinct? | Biggest Snake Ever | Dr Binocs Show | Peekaboo Kidz
If Audioslave wrote 'The Show Must Go On'
If you lift this, i wil go home ! #fyp #frank #anatolyprank #anatoly #gym #gymmotivation #foryou
10-Year-Old Billie Eilish Would Go CRAZY If She Knew This...
If all humans died, when would the last light go out?
Proof that G is an Abelian Group if f(a) = a^(-1) is a Homomorphism
Комментарии
 0:02:57
0:02:57
 0:04:05
0:04:05
 0:01:42
0:01:42
 0:00:44
0:00:44
 0:23:07
0:23:07
 0:04:45
0:04:45
 0:09:56
0:09:56
 0:03:39
0:03:39
 0:00:08
0:00:08
 0:01:22
0:01:22
 0:05:09
0:05:09
 0:01:35
0:01:35
 0:03:31
0:03:31
 0:05:55
0:05:55
 0:00:12
0:00:12
 0:04:10
0:04:10
 0:03:03
0:03:03
 0:04:45
0:04:45
 0:05:43
0:05:43
 0:02:26
0:02:26
 0:01:00
0:01:00
 0:00:20
0:00:20
 0:00:55
0:00:55
 0:08:22
0:08:22