filmov
tv
Proof that if g o f is Surjective(Onto) then g is Surjective(Onto)
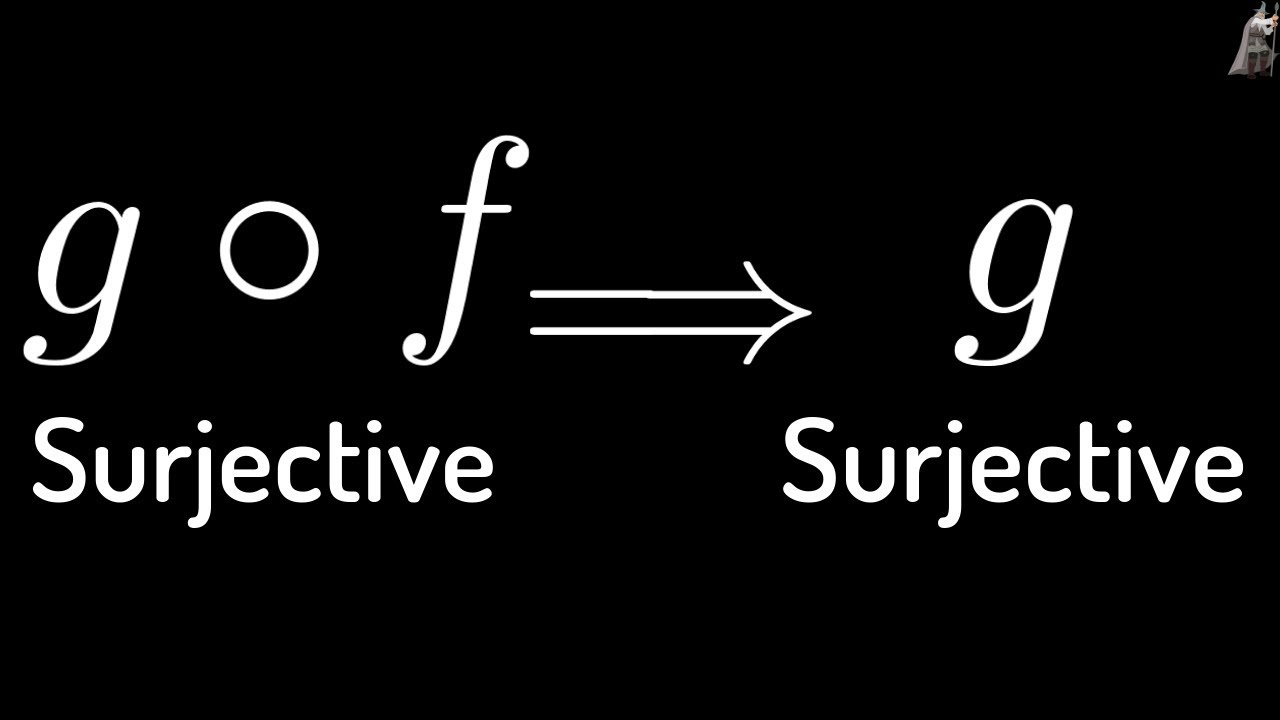
Показать описание
Proof that if g o f is Surjective(Onto) then g is Surjective(Onto). Given two functions f : A to B and g: B to C, we prove that if the composition g o f: A to C is a surjective function then g is also surjective function.
If US and China Go To War, Who Loses (Hour by Hour)
Proof that if g o f is Surjective(Onto) then g is Surjective(Onto)
Proof that o(x) divides |G| if G is Finite
Group Theory Proof: If g^n = e then the order of g divides n
Proof that f(a) = a^(-1) is a Group Isomorphism if G is Abelian
Westlife - If I Let You Go (Lyrics)
What If Titanoboa Snake Didn't Go Extinct?
If G is Cyclic so is G/H Proof
Iqtidar Episode 27 [ENG CC] Anmol Baloch - Ali Raza - 19th December 2024 - Green TV Entertainment
If US and Russia Go To War, Who Loses (Hour by Hour)
If Israel and Iran Go to War - Who Wins?
If You Go To HELL…(DO THIS) 🤯👹 #shorts #hell #christian
If You Go to This Backrooms Level ALONE... YOU'RE DEAD.
If I go down, we go down together 🥰 @asherlara #sofimanassyan #relatable #friends
If I Go Away
Angie Martinez ft. Lil' Mo & Sacario – If I Could Go! (Official Video)
Would you go to school if… Amp World edition
What If The Titanoboa Didn't Go Extinct? | Biggest Snake Ever | Dr Binocs Show | Peekaboo Kidz
Kelsea Ballerini - IF YOU GO DOWN (I'M GOIN' DOWN TOO) [Official Music Video]
If x^2 = e for all x in G then G is an abelian group proof
If I Go, I'm Goin - Gregory Alan Isakov with Aoife O'Donovan & Chris Thile | Live from...
Tom Waits - 'If I Have To Go'
If I Go
Proof that G is an Abelian Group if f(a) = a^(-1) is a Homomorphism
Комментарии
 0:26:34
0:26:34
 0:02:57
0:02:57
 0:01:42
0:01:42
 0:04:05
0:04:05
 0:09:56
0:09:56
 0:03:39
0:03:39
 0:10:04
0:10:04
 0:03:31
0:03:31
 0:39:08
0:39:08
 0:53:10
0:53:10
 0:23:04
0:23:04
 0:00:28
0:00:28
 0:08:15
0:08:15
 0:00:12
0:00:12
 0:05:18
0:05:18
 0:04:10
0:04:10
 0:00:36
0:00:36
 0:05:43
0:05:43
 0:03:08
0:03:08
 0:01:35
0:01:35
 0:04:45
0:04:45
 0:02:16
0:02:16
 0:05:26
0:05:26
 0:08:22
0:08:22