filmov
tv
If x^2 = e for all x in G then G is an abelian group proof
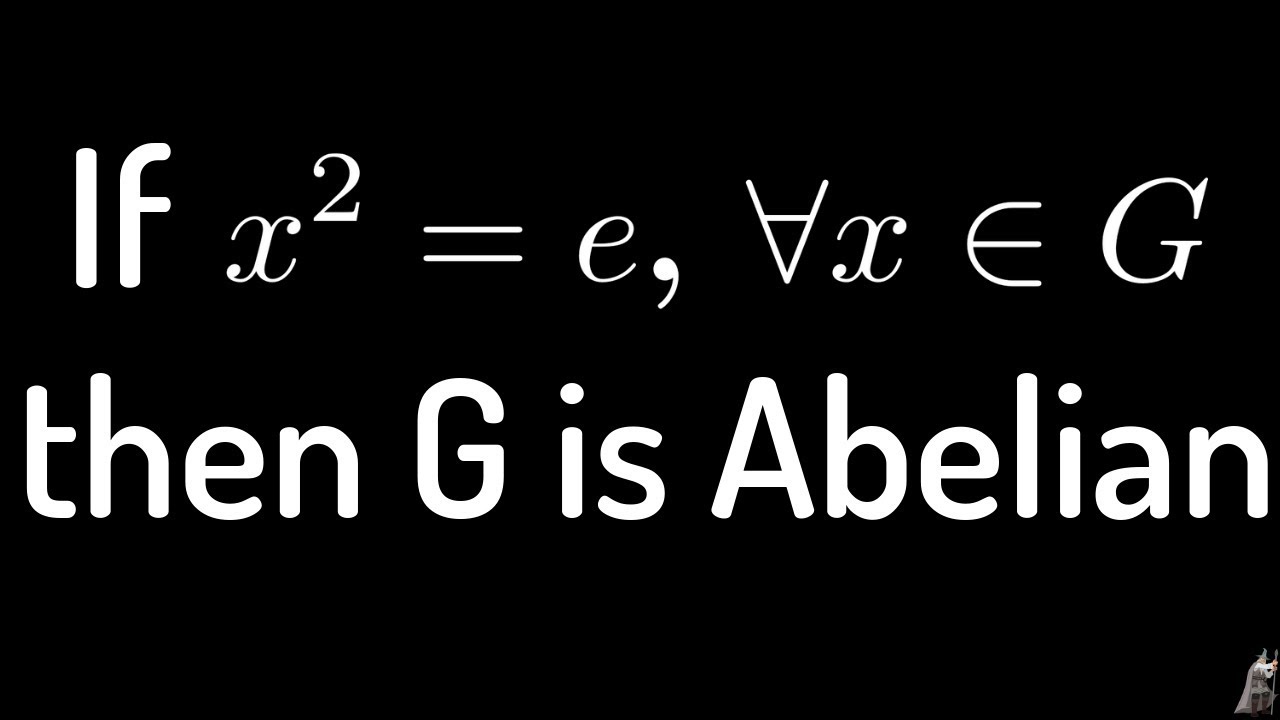
Показать описание
If x^2 = e for all x in G then G is an abelian group proof
If x^2 = e for all x in G then G is an abelian group proof
B6) Var(X)=E(X^2)-[E(X)]^2
Math secret your teacher won't tell you
Derivative of y = e^(x^2)
improper integral of x*e^(-x^2) from -inf to +inf
When is e^x=x^2? (ft. Lambert W Product Logarithm) #shorts
ALL solutions to x^2=2^x
Every Student Should See This
If the sum of all the roots of e^2x-11e^x-45e^(-x)+81/2=0 is log_ep, then p | AOD | #jee #jeemains...
H={x^2=e} is Subgroup of an Abelian group Proof |Maths |Mad Teacher
Can You Solve for X in 5^x=2e^x? | Exponential Equation | SAT Math Problem
The function \( f(x)=x(x+3) e^{-x / 2} \) satisfies all the conditi...
Find the Derivative of f(x) = 2e^(7x)
How to use Tabular Integration Example with x^2*e^x #shorts
An Integral with e^x
Integrating Exponential Functions By Substitution - Antiderivatives - Calculus
Learn how to evaluate for a function
PreCalculus - Logarithmic & Exponential Functions (3 of 20) x=? for [e^(2x)]-(3e^x)-10=0
The function f(x)= x(x+3)e^-1/2x satisfy all the conditions of Rolles theorem in [-3,0]. c value is
Proof that the Sample Variance is an Unbiased Estimator of the Population Variance
Derivative of f(x) = e^x/x^2
Integral of x^2e^-x^2 from 0 to infinity. 💪
E(Y)=aE(x) +b and V(Y) =a^2V(Y) where Y=aX+b / problems on continues random variables
The interval in which y = x^2e^-x is increasing a) (-∞, ∞) b) (-2, 0) c) (2, ∞) d) (0, 2)
Комментарии
 0:01:35
0:01:35
![B6) Var(X)=E(X^2)-[E(X)]^2](https://i.ytimg.com/vi/_vv5EwvOQXk/hqdefault.jpg) 0:01:51
0:01:51
 0:12:16
0:12:16
 0:02:25
0:02:25
 0:05:20
0:05:20
 0:01:00
0:01:00
 0:13:21
0:13:21
 0:00:58
0:00:58
 0:03:07
0:03:07
 0:03:21
0:03:21
 0:04:12
0:04:12
 0:06:21
0:06:21
 0:00:44
0:00:44
 0:00:34
0:00:34
 0:00:51
0:00:51
 0:11:16
0:11:16
 0:02:15
0:02:15
 0:02:14
0:02:14
 0:03:21
0:03:21
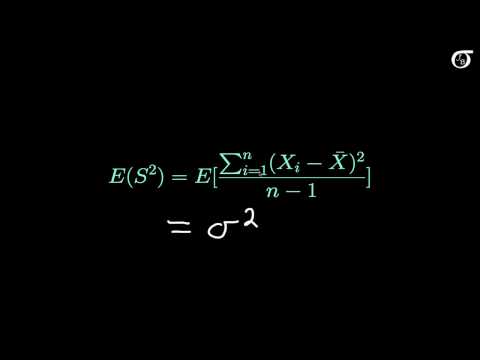 0:06:58
0:06:58
 0:02:59
0:02:59
 0:03:59
0:03:59
 0:06:00
0:06:00
 0:02:34
0:02:34