filmov
tv
If G is a group, then (a^-1)^-1=a for all a in G.

Показать описание
Theorems in Group Theory
Groups - Showing G is a group - Part 1
Proof that f(a) = a^(-1) is a Group Isomorphism if G is Abelian
Group Theory Proof: If g^n = e then the order of g divides n
12. If G is a group such that x.x=e for all x∈G then G is an abelian group
If G is a group such that (ab)^n=(a)^n(b)^n for three consecutive integers n for all a,b in G show
If G is a group, prove that for all a,b in G, (ab)^{-1}= b^{-1}a^{-1}
Proof that G is an Abelian Group if f(a) = a^(-1) is a Homomorphism
if G be finite group and a be any element of G s.t. o(a)=n them a^m=e iff n|m
if f is a homomorphism of a group g into a group g' with kernel k then k is a normal subgroup o...
If G is Abelian Group Then It's Every SubGroup is Normal in G| Group Theory|M.Asif Math Corner
18. If G is a group and it has only element 'a' whose order is 2 then ax=xa
If G is a group, then (a^-1)^-1=a for all a in G.
If in a group G * a ^ 5 = e aba^-1= b^2 for a, b belongs to G then show that o(b) = 31
if G/Z(G) is Cyclic group then G is an Abelian group.
If a is a generator of a cyclic group G, then it’s inverse is also a generator.
40. If G is a cyclic group of order 24 find the order of elements e,a^9,a^10
Show that a group G is abelian if and only if (ab)^2=a^2b^2 for all a,b€G
If G is a group and H and K are subgroups of finite index in G, then HnK is of finite index in G .
Quotient Group | If G is a group and N is a normal subgroup of G, then G/N is a group
Show that a group 𝐺 is an abelian iff (ab)^2=a^2b^2 ,for all a,b∈𝐺
If G is a finite group whose order is prime, then G is a cyclic group .
If G be a Group,then (ab)'=b'a' /Group Theory/3rd sem/unit-1/Telugu expalination
If G is a group, prove that Z(G)= ⋂(a∈G)C(a)
44. Z(G)=G if and only if G is abelian group | Group Theory | AdnanAlig
Комментарии
 0:05:35
0:05:35
 0:09:56
0:09:56
 0:04:05
0:04:05
 0:04:52
0:04:52
 0:00:16
0:00:16
 0:03:14
0:03:14
 0:08:22
0:08:22
 0:08:36
0:08:36
 0:02:32
0:02:32
 0:04:59
0:04:59
 0:05:55
0:05:55
 0:01:22
0:01:22
 0:00:06
0:00:06
 0:11:06
0:11:06
 0:07:10
0:07:10
 0:10:31
0:10:31
 0:00:16
0:00:16
 0:14:03
0:14:03
 0:11:52
0:11:52
 0:04:28
0:04:28
 0:03:35
0:03:35
 0:07:08
0:07:08
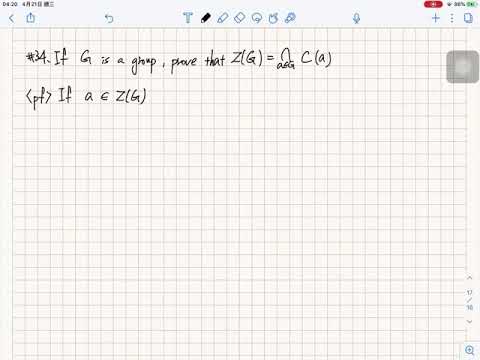 0:00:55
0:00:55
 0:02:59
0:02:59