filmov
tv
What do Matrices Represent? - Learning Linear Algebra

Показать описание
This video is about why we use matrices and how every matrix is related to a function that takes vectors as inputs. Understanding what a matrix represents is important in order to learn about the more advanced ideas in linear algebra!
Subscribe to see more new math videos!
Music: OcularNebula - The Lopez
Subscribe to see more new math videos!
Music: OcularNebula - The Lopez
What do Matrices Represent? - Learning Linear Algebra
Linear transformations and matrices | Chapter 3, Essence of linear algebra
1: What Does a Matrix Represent? - Learning Linear Algebra
Understanding Matrices and Matrix Notation
Dear linear algebra students, This is what matrices (and matrix manipulation) really look like
Matrices: Why they even exist?
Tate explains matrices in 90 seconds
Intro to Matrices
The determinant | Chapter 6, Essence of linear algebra
Eigenvectors and eigenvalues | Chapter 14, Essence of linear algebra
What is a determinant?
Representing data with matrices | Matrices | Precalculus | Khan Academy
Matrix Transformations : reflections and rotations
Graph Representation with an Adjacency Matrix | Graph Theory, Adjaceny Matrices
Linear Algebra 19k: Matrix Representation of a Linear Transformation - Vectors in ℝⁿ
Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra
Boolean Matrix Multiplication: Easy to Follow Example!
Linear transformations | Matrix transformations | Linear Algebra | Khan Academy
Linear Transformations on Vector Spaces
Why do we multiply matrices the way we do??
What eigenvalues and eigenvectors mean geometrically
Using Matrices to Represent Information
Transformation matrix with respect to a basis | Linear Algebra | Khan Academy
Using Matrices to Represent Data
Комментарии
 0:12:01
0:12:01
 0:10:59
0:10:59
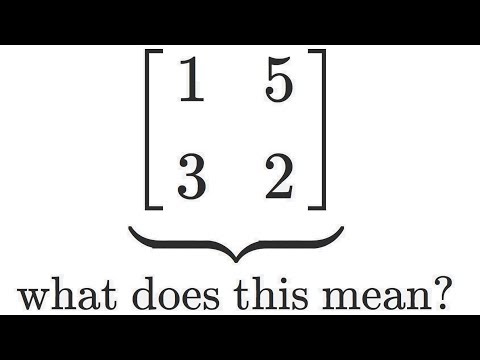 0:09:06
0:09:06
 0:05:26
0:05:26
 0:16:26
0:16:26
 0:09:31
0:09:31
 0:01:30
0:01:30
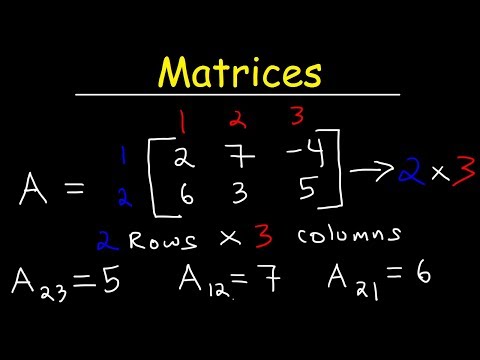 0:11:23
0:11:23
 0:10:03
0:10:03
 0:17:16
0:17:16
 0:02:51
0:02:51
 0:05:43
0:05:43
 0:03:26
0:03:26
 0:04:58
0:04:58
 0:12:40
0:12:40
 0:12:09
0:12:09
 0:03:18
0:03:18
 0:13:52
0:13:52
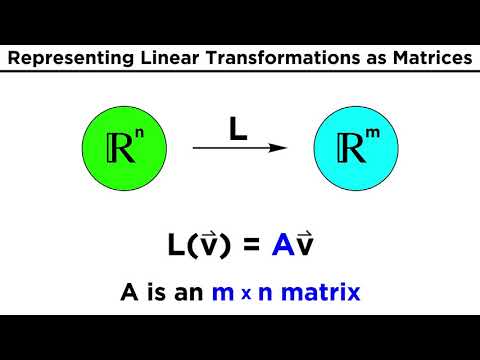 0:09:11
0:09:11
 0:16:26
0:16:26
 0:09:09
0:09:09
 0:02:32
0:02:32
 0:18:02
0:18:02
 0:05:08
0:05:08