filmov
tv
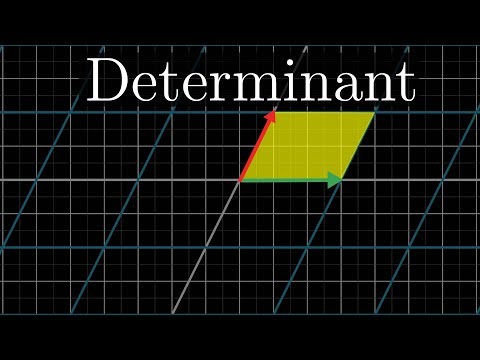
What is a determinant?

Показать описание
How do we interpret the determinant intuitively? Well, here is one way!
This video was requested by Thecalculatorman on reddit!
A few quick notes:
* There are limitations to this way of thinking about the determinant, but for the most part it's solid for 3 and 2D objects.
* Finding the area of the transformed unit cube is the same as finding the area of the parallelpiped, just a little easier to explain. In hindsight, I should have added this definition too.
* There is a lot I skipped over, like how to perform the determinant. That wasn't the point of this video. I wanted to give people an intuitive feel for what the determinant was doing underneath.
As always, the simulations were done live on:
Feel free to follow me on Twitter!
And the music is from Josh Woodward (sped up 1.5 times):
Thanks for watching!
Also, discord:
This video was requested by Thecalculatorman on reddit!
A few quick notes:
* There are limitations to this way of thinking about the determinant, but for the most part it's solid for 3 and 2D objects.
* Finding the area of the transformed unit cube is the same as finding the area of the parallelpiped, just a little easier to explain. In hindsight, I should have added this definition too.
* There is a lot I skipped over, like how to perform the determinant. That wasn't the point of this video. I wanted to give people an intuitive feel for what the determinant was doing underneath.
As always, the simulations were done live on:
Feel free to follow me on Twitter!
And the music is from Josh Woodward (sped up 1.5 times):
Thanks for watching!
Also, discord:
What is a determinant?
The determinant | Chapter 6, Essence of linear algebra
What is a Determinant?
Evaluating the Determinant of a Matrix
WHAT IS A DETERMINANT
Why is the determinant like that?
Matrix Determinants (1 of 3: Matrices as Vectors)
Interpreting determinants in terms of area | Matrices | Precalculus | Khan Academy
Future careers - Making right choices of careers based on personality types
Determinant of 3x3 Matrices, 2x2 Matrix, Precalculus Video Tutorial
Matrices | Determinant of a Matrix (Part 1) | Don't Memorise
What is a Determinant? (Matrices 4) | A-Level Further Maths
What is a determinant of a matrix?
Linear Algebra: Ch 2 - Determinants (1 of 48) What is a Determinant? (Part 1)
Oxford Linear Algebra: What is the Determinant Function for a Matrix?
Matrix Determinants (2 of 3: The Determinant's Geometric Meaning)
What is Determinant ? How To Find Determinants of a Matrix
Linear Algebra: Ch 2 - Determinants (3 of 48) What is a Determinant? (Part 3)
Linear Algebra: Ch 2 - Determinants (2 of 48) What is a Determinant? (Part 2)
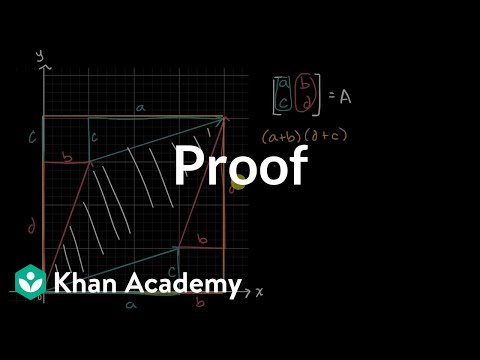
Proof: Matrix determinant gives area of image of unit square under mapping | Matrices | Khan Academy
What is the determinant of a matrix?
Linear Algebra 14a: Why Determinants?
Linear Algebra: Ch 2 - Determinants (4 of 48) What is a Determinant? (Part 4)
Lecture 1:- What is a determinant and how to solve a second order determinant.
Комментарии
 0:02:51
0:02:51
 0:10:03
0:10:03
 0:11:51
0:11:51
 0:07:09
0:07:09
 0:00:51
0:00:51
 0:19:07
0:19:07
 0:07:08
0:07:08
 0:04:19
0:04:19
 0:03:43
0:03:43
 0:10:17
0:10:17
 0:01:33
0:01:33
 0:12:13
0:12:13
 0:04:09
0:04:09
 0:03:19
0:03:19
 0:26:43
0:26:43
 0:10:35
0:10:35
 0:01:37
0:01:37
 0:05:26
0:05:26
 0:05:19
0:05:19
 0:04:19
0:04:19
 0:08:18
0:08:18
 0:05:11
0:05:11
 0:02:06
0:02:06
 0:09:06
0:09:06