filmov
tv
Linear Algebra 19k: Matrix Representation of a Linear Transformation - Vectors in ℝⁿ

Показать описание
Linear Algebra 19k: Matrix Representation of a Linear Transformation - Vectors in ℝⁿ
Linear Algebra - Lecture 19 - The Matrix of a Linear Transformation
How to Find the Matrix of a Linear Transformation
Transformation matrix with respect to a basis | Linear Algebra | Khan Academy
Linear Algebra - Lecture 17 - Matrix Transformations
Linear Algebra 19g: Matrix Representation of a LT - the Algorithm Works!
How to Determine Standard Matrix of Linear Transformation - Linear Algebra
Linear Algebra 19f: The Heart of Component Spaces - Matrix Representation of a Linear Tranformation
Linear Transformations on Vector Spaces
1: What Does a Matrix Represent? - Learning Linear Algebra
Matrix Representation of linear operator II Introduction to Linear Algebra
Matrix Representations of Linear Transformation
Linear Algebra 19j: Matrix Representation of a Linear Transformation - Polynomials
Linear Algebra 19L: Matrix Representation of a LT - Vectors in ℝⁿ, Standard Basis
Linear transformations as matrix vector products | Linear Algebra | Khan Academy
Linear Algebra | Linear Transformations and Matrix Representations
#5||Matrix representation of Linear Transformation||Linear algebra||maths for graduates
Matrix representation -- Example
Matrix-Representation of Linear Mappings
Linear Algebra 19o: Matrix Representation of a LT - Better than an Eigenbasis?
Linear Algebra Example Problems - Finding 'A' of a Linear Transformation #2
Linear Algebra 19m: Matrix Representation of a LT - Vectors in ℝⁿ, Eigenbasis
Linear Algebra 19h: Matrix Representation of a Linear Transformation - Alternative Basis
Lecture 61: Linear Algebra (Matrix representations of linear transformations)
Комментарии
 0:12:40
0:12:40
 0:10:44
0:10:44
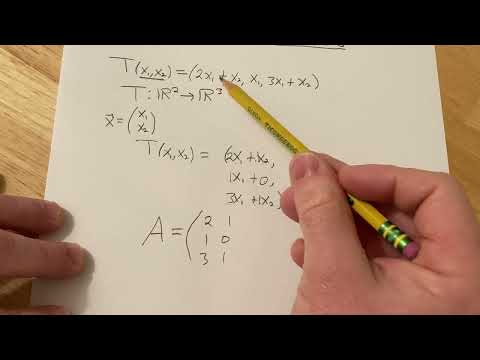 0:05:19
0:05:19
 0:18:02
0:18:02
 0:11:32
0:11:32
 0:06:22
0:06:22
 0:14:15
0:14:15
 0:14:34
0:14:34
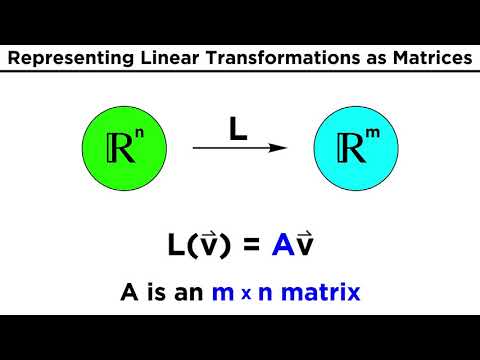 0:09:11
0:09:11
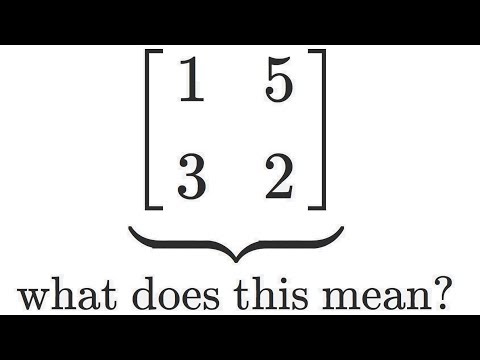 0:09:06
0:09:06
 0:10:18
0:10:18
 0:13:08
0:13:08
 0:10:19
0:10:19
 0:03:46
0:03:46
 0:17:32
0:17:32
 0:08:08
0:08:08
 0:05:32
0:05:32
 0:04:02
0:04:02
 0:30:05
0:30:05
 0:05:23
0:05:23
 0:07:40
0:07:40
 0:11:12
0:11:12
 0:09:07
0:09:07
 0:29:36
0:29:36