filmov
tv
Visualizing the derivative of sin(x)

Показать описание
A visual of the derivative of f(x)=sin(x). We show how to think about the derivative of a function visually.
#manim #calculus #derivatives #derivative #tangentline #slope #parabola #mathvideo #mathshorts #math #visualmath #graph #sinefunction #trigonometry #linearapproximation
#manim #calculus #derivatives #derivative #tangentline #slope #parabola #mathvideo #mathshorts #math #visualmath #graph #sinefunction #trigonometry #linearapproximation
Visualizing the derivative of sin(x)
Visual Calculus: Derivative of sin(θ) is cos(θ)
Visualizing the Derivative of sin(x)
Derivative of sin(x) | Animation | mathocube |
Proof: Derivative of Sin is Cos (Version 2)
Establishing the Derivatives of sin x, cos x & tan x
Derivative of sinx graphically using geogebra
Visualising derivative of sin(x) in Python/Pygame ||derivatives| |Calculus #python #pygame #visual
Visualizing the chain rule and product rule | Chapter 4, Essence of calculus
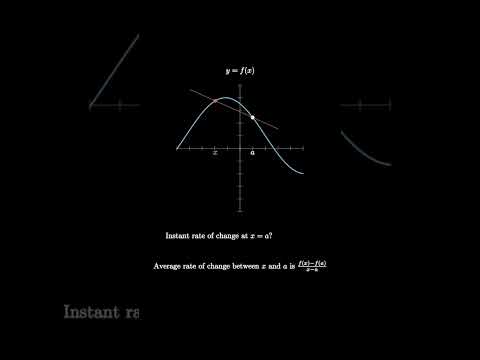
Visual Derivative Definition!
Visual derivative of x squared
Visualizing Trigonometry: Sine Function
Trig Visualized: One Diagram to Rule them All (six trig functions in one diagram)
derivative of sin(sin(x)) #apcalculus
Proof of the derivative of sinx: A Step-by-Step Proof and Explanation
Trigonometry Concepts - Don't Memorize! Visualize!
Visualization of the derivative of the cosine function. Animation of the derivative as a function.
Visualizing The Derivative of cos(x) Animated
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
How REAL Men Integrate Functions
Sine Curve and the Unit Circle
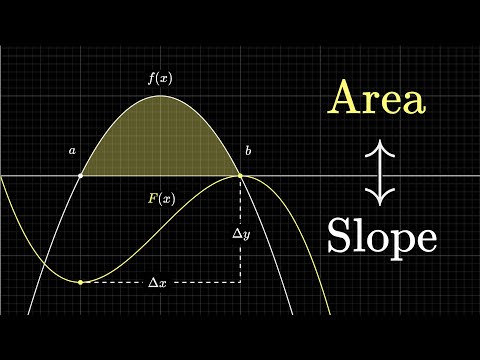
What does area have to do with slope? | Chapter 9, Essence of calculus
The PROOF that the Derivative of sin(x) is cos(x)!!! | Limit Definition of Derivatives
Derivative of sin x & cos x | AP Calculus | Calculus 1 #shorts
Комментарии
 0:00:59
0:00:59
 0:03:08
0:03:08
 0:00:33
0:00:33
 0:01:37
0:01:37
 0:09:39
0:09:39
 0:17:08
0:17:08
 0:00:15
0:00:15
 0:01:23
0:01:23
 0:15:56
0:15:56
 0:01:00
0:01:00
 0:00:58
0:00:58
 0:01:12
0:01:12
 0:04:15
0:04:15
 0:00:14
0:00:14
 0:06:06
0:06:06
 0:32:35
0:32:35
 0:00:15
0:00:15
 0:00:17
0:00:17
 0:00:38
0:00:38
 0:00:35
0:00:35
 0:00:27
0:00:27
 0:12:39
0:12:39
 0:03:47
0:03:47
 0:00:48
0:00:48