filmov
tv
Does Derivative Have to be Continuous? (feat. x^2sin(1/x))
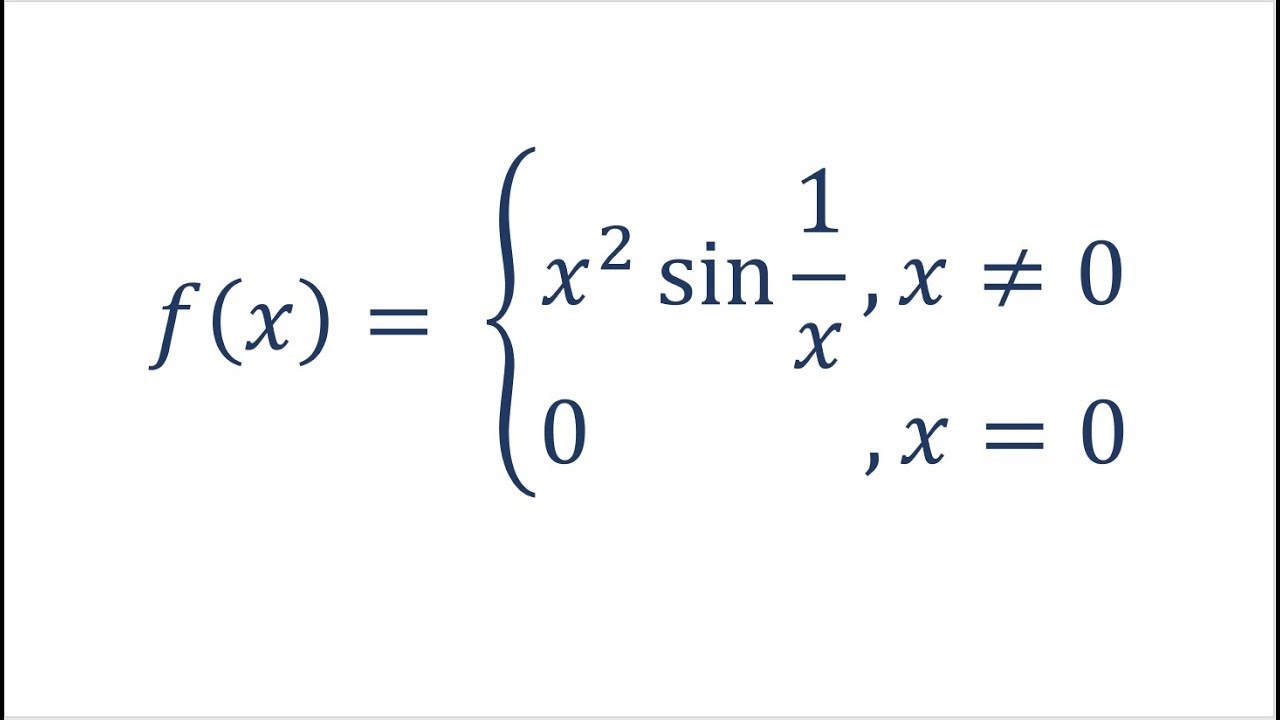
Показать описание
If our function is continuous AND differentiable, does derivative have to be continuous as well?
Your support is truly a huge encouragement.
Please take a second to subscribe in order to send us your valuable support and receive notifications for new videos!
Every subscriber and every like are wholeheartedly appreciated.
Your support is truly a huge encouragement.
Please take a second to subscribe in order to send us your valuable support and receive notifications for new videos!
Every subscriber and every like are wholeheartedly appreciated.
Derivative as a concept | Derivatives introduction | AP Calculus AB | Khan Academy
What does area have to do with slope? | Chapter 9, Essence of calculus
Visual Derivative Definition!
Derivatives Explained in One Minute
The paradox of the derivative | Chapter 2, Essence of calculus
What does the second derivative actually do in math and physics?
Where a function is not differentiable | Taking derivatives | Differential Calculus | Khan Academy
What is a derivative?
When Does a Function Not Have a Derivative?
Does Derivative Have to be Continuous? (feat. x^2sin(1/x))
Understand Calculus in 35 Minutes
What is a Derivative? Deriving the Power Rule
Alternate Form of The Limit Definition of the Derivative - Calculus
Difference Between Partial and Total Derivative
Why isn't abs(x) differentiable at x=0? (definition of derivative)
Definition of the Derivative
When Does A Derivative Not Exist?
Derivatives: Crash Course Physics #2
Higher order derivatives | Chapter 10, Essence of calculus
The meaning behind the first and second derivative
The essence of calculus
ARE YOU A PRINCIPAL OR DERIVATIVE APPLICANT? | With Examples
What is Jacobian? | The right way of thinking derivatives and integrals
Calculus 1 - Derivatives
Комментарии
 0:07:16
0:07:16
 0:12:39
0:12:39
 0:01:00
0:01:00
 0:01:30
0:01:30
 0:16:50
0:16:50
 0:15:19
0:15:19
 0:03:35
0:03:35
 0:10:43
0:10:43
 0:04:47
0:04:47
 0:09:04
0:09:04
 0:36:22
0:36:22
 0:10:05
0:10:05
 0:08:10
0:08:10
 0:01:44
0:01:44
 0:09:02
0:09:02
 0:23:31
0:23:31
 0:07:05
0:07:05
 0:10:02
0:10:02
 0:05:39
0:05:39
 0:02:55
0:02:55
 0:17:05
0:17:05
 0:09:39
0:09:39
 0:27:14
0:27:14
 0:52:51
0:52:51