filmov
tv
Alternating Geometric Series Sum

Показать описание
This is a short, animated visual proof demonstrating the infinite alternating geometric series formula for any positive ratio r with r less than 1 and with positive first term a. This series is important for many results in calculus, discrete mathematics, and combinatorics.
Thanks!
#mathshorts #mathvideo #math #calculus #mtbos #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #geometricsums #series #infinitesums #infiniteseries #geometric #geometricseries
To learn more about animating with manim, check out:
Thanks!
#mathshorts #mathvideo #math #calculus #mtbos #manim #animation #theorem #pww #proofwithoutwords #visualproof #proof #iteachmath #geometricsums #series #infinitesums #infiniteseries #geometric #geometricseries
To learn more about animating with manim, check out:
Alternating Geometric Series Sum
Alternating Geometric Series: sum of Powers of 1/2 (visual proof)
Geometric Series: Alternating Sum of Powers of 1/4 (visual proof)
Finding the sum of a series with alternating terms
Alternating Geometric Series: Powers of -1/3 (visual proof)
Find the sum of an alternating geometric series where sequence is -13, 39, ... -9477.
Geometric Series | Convergence, Derivation, and Example
Alternating Geometric Series (visual proof)
Alternating Geometric Series: sum of powers of 1/2 II (visual proof)
Alternating infinite sum!
Finding The Sum of an Infinite Geometric Series
Ex: Determine if an Alternating Infinite Geometric Series Converges or Diverges
(5.2.29) Deciphering an Alternating Geometric Series: From Summation to Closed Form
Calculus 2 - Geometric Series, P-Series, Ratio Test, Root Test, Alternating Series, Integral Test
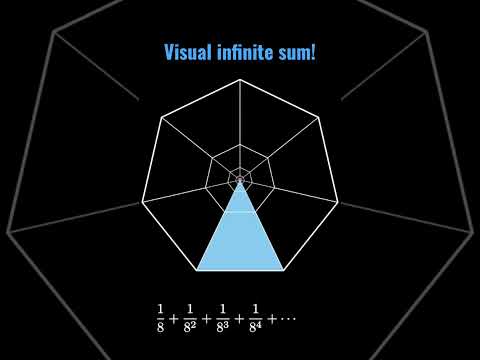
Summing powers of 1/8 visually!
Geometry of the Alternating Harmonic Series (visual proof)
How to find the sum of almost any rearrangement of the alternating harmonic series.
Geometric series convergence and divergence examples | Precalculus | Khan Academy
Telescoping Series
Summing The Alternating Harmonic Series
Alternating Series Test
Geometry behind the geometric sum of powers of 1/3!
Choosing Which Convergence Test to Apply to 8 Series
A visual alternating sum!
Комментарии
 0:01:00
0:01:00
 0:01:28
0:01:28
 0:01:26
0:01:26
 0:04:02
0:04:02
 0:01:43
0:01:43
 0:04:22
0:04:22
 0:06:28
0:06:28
 0:02:06
0:02:06
 0:01:58
0:01:58
 0:00:52
0:00:52
 0:19:50
0:19:50
 0:05:05
0:05:05
 0:02:27
0:02:27
 0:43:52
0:43:52
 0:00:53
0:00:53
 0:04:20
0:04:20
 0:00:50
0:00:50
 0:07:08
0:07:08
 0:23:39
0:23:39
 0:09:32
0:09:32
 0:19:41
0:19:41
 0:01:00
0:01:00
 0:12:13
0:12:13
 0:00:51
0:00:51