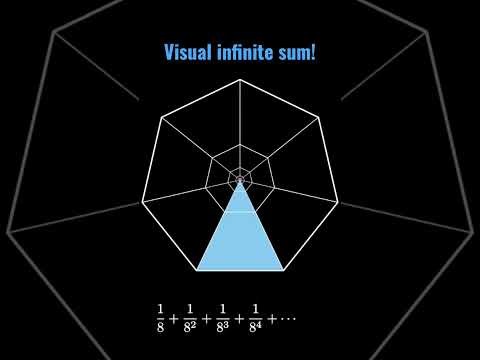
Summing powers of 1/8 visually!

This is a short, animated visual proof showing the sum of the infinite geometric series of powers of 1/8 (starting with 1/8) is 1/7 using self similar trapezoids in a regular heptagon. #manim #math​​ #mathshorts​ #mathvideo​ #mtbos​ #manim​ #animation​ #theorem​ #pww​ #proofwithoutwords​ #visualproof​ #proof​ #iteachmath #calculus #series #geometricseries #infiniteseries #heptagon #trapezoids

To learn more about animating with manim, check out:

[dpride]

"Start with a regular heptagon"

Me, A compass and straightedge user: "A what?"

[hedgehogmorph]

I wonder why it still isn't here:
An infinite number of mathematicians walk into a bar. The first one orders half a beer. The second orders quarter of a beer. Next, an eighth of a beer...
"Hold up yobs!", the bartender interrupts disgruntledly: "Here - you can take this one pint and sort it out yourselves"

[sebastianalancliffordthomp]

Thinking about it, this works for any regular shape, so the sum of (1/x)^i = 1/(x-1) for everything down to x=4 since a triangle is the smallest regular shape.

[aboxthatdrools]

The YouTube algorithm is making me learn math.

[Miftahul_]

If anyone wants the formula, this type of thing is called an infinite geometric sum, also known as a geometric series. The formula is a/(1-r) where “a” is the first term and “r” is the common ratio. Here, a is 1/8 and r is also 1/8 as that’s what you’re multiplying by every next term. Put it into the formula and you get 1/8/(1-1/8) which is the same as 1/(8(1-1/8)) which expands to 1/7 so it is indeed true to infinity. For the more general sum up to “n” amount of terms, you can use the formula a(1-r^n)/(1-r).

[monkapaul]

Let, r = 1/8 + 1/8² + 1/8³ + 1/8⁴ + ...

Now multiply both sides with 8

=> 8r = 1 + 1/8 + 1/8² + 1/8³ + 1/8⁴ +...
Or, 8r = 1 + r
Or, 8r - r = 1
Or, 7r = 1
Therefore, r = 1/7

[alexkz]

This thing went from Star Wars to resident evil in two seconds flat

[ruthvikas]

Is it like the series for any number N be like
1/N + 1/N² + 1/N³ + ... = 1/(N-1) ?

[sandwich]

I love solving math visually, it just makes alot of sense and it helps others understand it more

[humzahkhan]

Thats acc a really intuitive proof. Honestly, it helps me understand how this can be generalized as well to any regular polygon above a square i think

[Gelfling]

This is a fantastic visual. I learned sums in highschool and even though I could do them, I could write them out and solve them, I didn't know what I was doing or understand it. This gives an amazing visual I wish I had back then

[moadrawingworld]

Ramanujan Infinite Series
If you take 1/8 out, infinite series wont change thus
1/8(S+1) = S
Where S is infinite series mentioned
Thus S = 1/7

[AlbinoJedi]

That was so well explained I'm impressed.

[DanGRV]

I feel conflicted about these polygonal constructions.

On one hand, these work for every polygon (n=3 or greater) to show the result for the geometric series with ratio 1/(n+1), and I love that.

On the other hand, it feels arbitrary that the middle polygon in each step has to have an area of 1/(n+1) times the area of the previous step. What happens if for each step we choose a different factor? Let's call that sequence of factors r_k.

What happens is that we get a telescoping sum which depends on the limit of the products r_1 * r_2 * r_3 * ... * r_k

Explicitly, the sum of the areas of the trapezoids is

S = (1/n) * (1 - (product from k=1 to infinity of r_k))

In the particular case of constant factors (r_k=1/(n+1)) the infinite product goes to zero and we get that S = 1/n

But many other sequences of factors r_k give the same result with the construction looking pretty much the same, which makes me consider it somewhat "misleading". That's the part I don't like about it

[thomaskaldahl]

I may have commented this before on another vid, but this channel/proof type is literally what allowed me to figure out why it's called a *geometric* series :D

[derblaue]

Damn, I found no one in the comments that says "It's just infinetly smaller then 1/7, it never becomes 1/7" and I think that's beautiful.

[mutatedllama]

I am so glad I found this. Visual proofs were never really taught when I did my maths degree and sometimes I found it so hard. It's amazing how much easier it is with stuff like this. Thank you!

[JgHaverty]

Oh my god that visual example makes it so intuitive

[Schrodinger_]

This would work if you make the inner heptagon any fraction you want. For example, if your inner heptagon has area 1/n, then each of the 7 slices outside it has area (n-1)/7n. Then the infinite series for that shaded part would be (n-1)/7n * sum_k (1/n)^k = n/(n-1). Thus the total shaded region is [(n-1)/7n] * [n/(n-1)] = 1/7

[teeweezeven]

Wow, you can make infinitely many videos like this!