filmov
tv
Finding the sum of a series with alternating terms
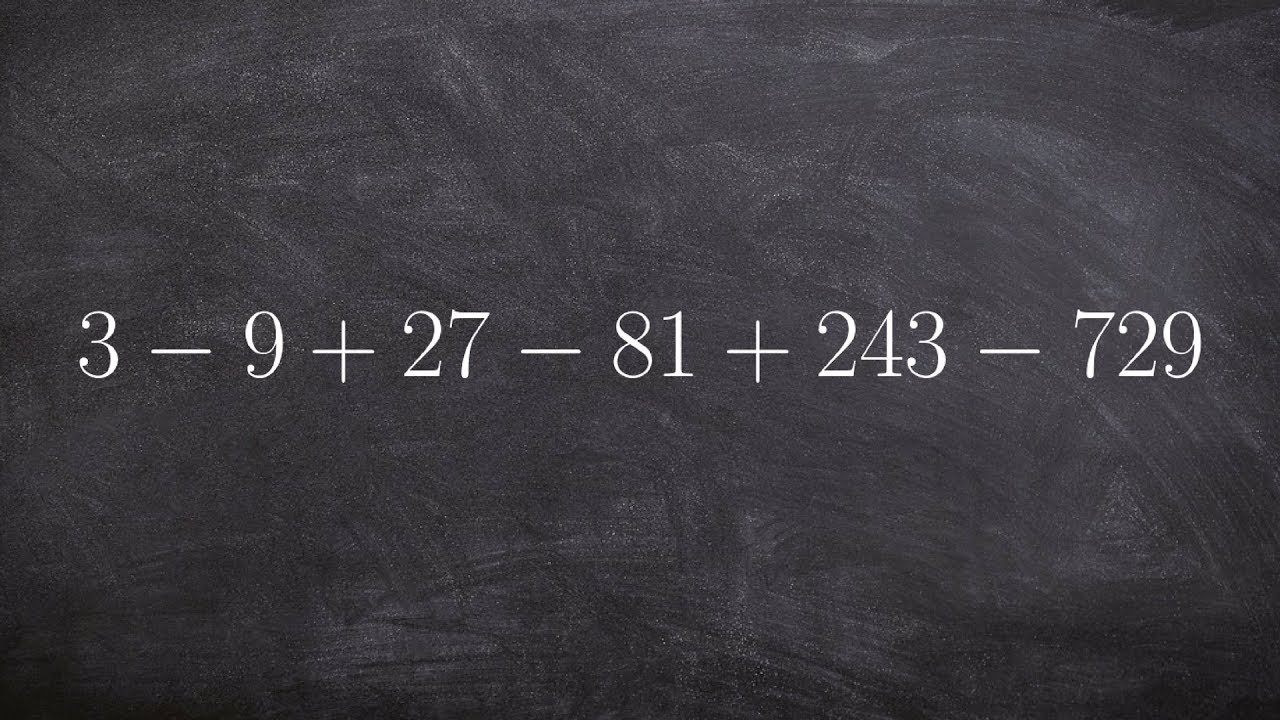
Показать описание
👉 Learn how to find the geometric sum of a series. A series is the sum of the terms of a sequence. A geometric series is the sum of the terms of a geometric sequence. The formula for the sum of n terms of a geometric sequence is given by Sn = a[(r^n - 1)/(r - 1)], where a is the first term, n is the term number and r is the common ratio.
Organized Videos:
✅Series
✅Series | Learn About
✅Find the Sum of the Arithmetic Series
✅Find the Sum of the Geometric Series
✅Write the Rule of the Geometric Series
✅Find the Sum of a Series
✅Write the Rule of the Series
Connect with me:
#series #brianmclogan
Organized Videos:
✅Series
✅Series | Learn About
✅Find the Sum of the Arithmetic Series
✅Find the Sum of the Geometric Series
✅Write the Rule of the Geometric Series
✅Find the Sum of a Series
✅Write the Rule of the Series
Connect with me:
#series #brianmclogan
Finding the sum or an arithmetic series using summation notation
What is the sum of 3/4 and 2/3?
How to find the sum of 3 numbers
Finding The Sum of an Infinite Geometric Series
Math tutorial for determining the sum of an arithmetic series
How to find the sum of a mixed number and a fraction
Finding the Sum of a Finite Arithmetic Series
Finding the sum of a series arithmetic
Find the sum of numbers given the average #maths #civilserviceexam #letreview #napolcom
Finding the Sum of a Series by Differentiating
Calculus II: Example finding the sum of a convergent series
Find the sum of coefficients
Evaluating the partial sum of a arithmetic series
Sum and Difference
How to Find the Sum of a Telescoping Series
Finding The Sum of a Finite Geometric Series
How to Find the Sum of Functions | Algebra, Adding Functions, Sums of Functions
How To Derive The Formula For The Sum of an Arithmetic Series
How To Find The Sum of a Geometric Series
What is the sum of an arithmetic series using the sum formula
Learn how to determine the sum of a geometric finite series
Evaluating the sum of an infinite series
How to Find the Exact Sum of a Series using Taylor Series | Series | Calculus | Glass of Numbers
Find the sum of the following fractions
Комментарии
 0:03:53
0:03:53
 0:03:05
0:03:05
 0:01:04
0:01:04
 0:19:50
0:19:50
 0:06:37
0:06:37
 0:01:55
0:01:55
 0:09:56
0:09:56
 0:04:58
0:04:58
 0:01:00
0:01:00
 0:04:01
0:04:01
 0:06:41
0:06:41
 0:05:07
0:05:07
 0:04:12
0:04:12
 0:01:36
0:01:36
 0:08:46
0:08:46
 0:12:59
0:12:59
 0:04:28
0:04:28
 0:06:38
0:06:38
 0:05:14
0:05:14
 0:02:44
0:02:44
 0:02:42
0:02:42
 0:02:01
0:02:01
 0:14:55
0:14:55
 0:03:20
0:03:20