filmov
tv
Summing The Alternating Harmonic Series
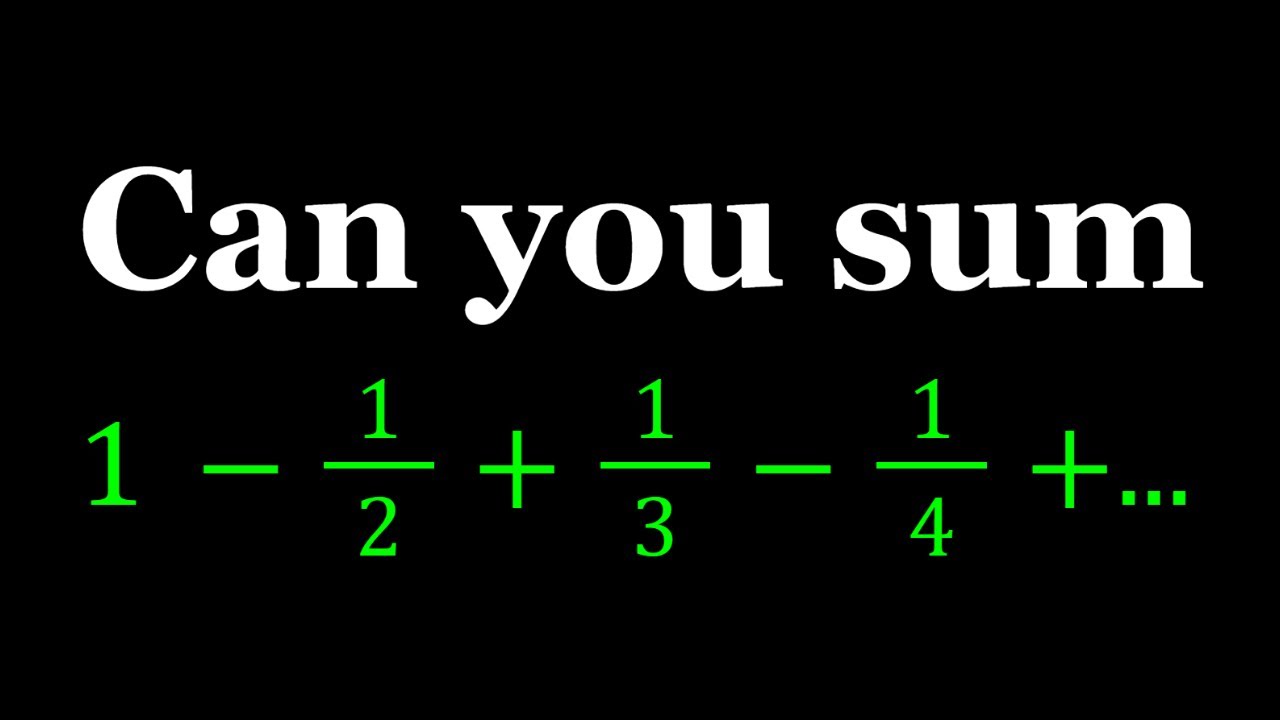
Показать описание
🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #SequencesAndSeries
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
GOOD LINKS:
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #SequencesAndSeries
via @YouTube @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
GOOD LINKS:
Summing The Alternating Harmonic Series
Geometry of the Alternating Harmonic Series (visual proof)
A nice approach to the alternating harmonic series
Clever Tricks with the Alternating Harmonic Series: Rearrangement Strategies
This Sum Amazes Me Every Time
The Mindblowing Alternating Harmonic Series
2023 Number Challenge: Estimate the Alternating Harmonic Series
Harmonic Series
700 years of secrets of the Sum of Sums (paradoxical harmonic series)
Visual Harmonic Series Divergence from Bernoulli!
alternating harmonic series
the alternating harmonic series
IMO 1979 Problem 1: Alternating Harmonic Series
Generalized alternating harmonic series integral
Alternating Series Test
Harmonic Sums and Divergence of Harmonic Series (visual proof)
Finding the sum of the alternating harmonic series
The Alternating Harmonic Series #1
Alternating Harmonic Series, Even and Odd
Easy Proof Of Summation of Alternating Harmonic Series
A visual infinite sum like you’ve never seen!
Alternating Series Test (AST) - Alternating Harmonic Series | Series | Calculus | Glass of Numbers
8.2 Harmonic Series vs Alternating Harmonic Series
Alternating series test and application to the alternating harmonic series (-1)^n-1/n.
Комментарии
 0:09:32
0:09:32
 0:04:20
0:04:20
 0:09:30
0:09:30
 0:20:50
0:20:50
 0:04:21
0:04:21
 0:06:15
0:06:15
 0:04:45
0:04:45
 0:03:52
0:03:52
 0:46:34
0:46:34
 0:01:00
0:01:00
 0:05:30
0:05:30
 0:00:47
0:00:47
 0:02:40
0:02:40
 0:11:11
0:11:11
 0:19:41
0:19:41
 0:03:09
0:03:09
 0:03:09
0:03:09
 0:45:32
0:45:32
 0:02:02
0:02:02
 0:19:28
0:19:28
 0:00:57
0:00:57
 0:05:33
0:05:33
 0:16:26
0:16:26
 0:02:42
0:02:42