filmov
tv
Computing the Surface Area of a surface parametrically // Example 2 // Vector Calculus

Показать описание
We compute the surface area of a cylinder between two planes. We will use the parametric integral formula for surface area that we computed in the previous video in my vector calculus playlist (see below). The first step is to come up with a parameterization. Because of the cylinder it makes sense to use something based out of cylindrical coordinates. As this has a fixed radius, we use theta and z as our parameters.
MY VECTOR CALCULUS PLAYLIST:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
MY VECTOR CALCULUS PLAYLIST:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
Computing the Surface Area of a surface parametrically // Example 1 // Vector Calculus
Computing the Surface Area of an Implicitly Defined Surface
Computing the Surface Area of a surface parametrically // Example 2 // Vector Calculus
Area of Surfaces of Revolution | Derivation & Example
Surface Area and Volume: Cylinder
The Surface Area formula for Parametric Surfaces // Vector Calculus
Math Antics - Circles, Circumference And Area
Surface Area for Implicit & Explicit Surfaces // Vector Calculus
Math Antics - Area
Evaluating Surface Integrals
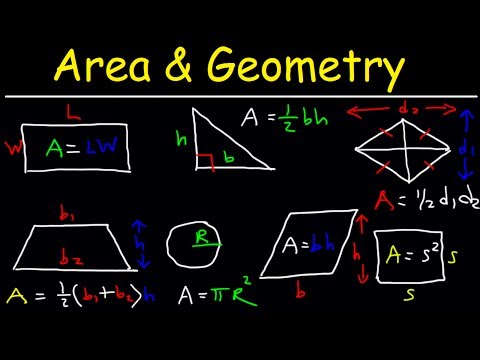
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geome...
Double integrals to find surface area (KristaKingMath)
Surface area of a box using nets
Solving Surface Area & Volume of a Rectangular Prism | Math in Minutes
Calculating the Surface Area of a Rectangular Prism
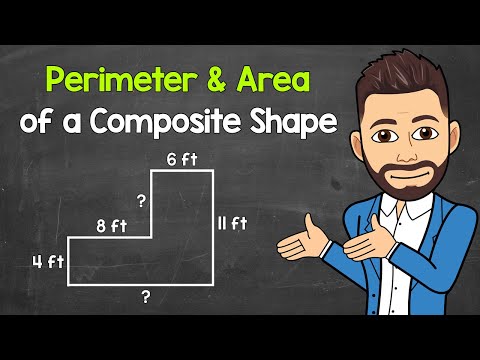
Finding the Perimeter and Area of a Composite Shape | L-Shaped Example | Geometry | Math with Mr. J
Area of a Triangle | MathHelp.com
KutaSoftware: PreAlgebra- Surface Area
Math Antics - Volume
Computing the Flux Across a Surface // Vector Calculus
Calculus 2: Area of a Surface of Revolution (Video #9) | Math with Professor V
Surface Area of Room
Multivariable Calculus | Surface area of a parameterized surface, example.
Area of a Trapezoid | MathHelp.com
Комментарии
 0:08:22
0:08:22
 0:07:13
0:07:13
 0:08:07
0:08:07
 0:08:29
0:08:29
 0:01:06
0:01:06
 0:09:26
0:09:26
 0:07:56
0:07:56
 0:08:13
0:08:13
 0:10:26
0:10:26
 0:12:24
0:12:24
 0:20:35
0:20:35
 0:12:12
0:12:12
 0:04:43
0:04:43
 0:03:34
0:03:34
 0:07:29
0:07:29
 0:08:21
0:08:21
 0:01:36
0:01:36
 0:44:52
0:44:52
 0:12:36
0:12:36
 0:08:09
0:08:09
 0:29:32
0:29:32
 0:09:09
0:09:09
 0:15:08
0:15:08
 0:01:39
0:01:39