filmov
tv
Computing the Surface Area of a surface parametrically // Example 1 // Vector Calculus

Показать описание
In this video we compute the surface area of the portion of a plane that lies within a cylinder. We've previously derived (see vector calculus playlist below) a formula to compute surface area for a parameterized surface, so our first ask is to find an appropriate parameterization of the plane. The key is that because the boundary is this cylinder, it makes sense to use the polar r and theta parameters so that our parameterization respects the boundary and will make the future integral easy to write down.
MY VECTOR CALCULUS PLAYLIST:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
MY VECTOR CALCULUS PLAYLIST:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
How to Find the Surface Area of a Rectangular Prism | Math with Mr. J
How to Find the Surface Area of a Cube | Math with Mr. J
How to Find the Surface Area of a Cylinder | Math with Mr. J
Computing the Surface Area of a surface parametrically // Example 1 // Vector Calculus
The Surface Area formula for Parametric Surfaces // Vector Calculus
Math Antics - Area
Volume of a Cylinder and Surface Area of a Cylinder
Surface Area of Revolution By Integration Explained, Calculus Problems, Integral Formula, Examples
Surface Area cut out by two cylinders, Multivariable Calculus
Computing the Surface Area of a surface parametrically // Example 2 // Vector Calculus
Surface Area and Volume: Cylinder
Surface Area of a Cone | Math with Mr. J
Computing the Surface Area of an Implicitly Defined Surface
Surface Area of a Pyramid - Lateral Area - Geometry
How to calculate the Surface Area - Maths Literacy
Math Antics - Circles, Circumference And Area
Area of Surfaces of Revolution | Derivation & Example
Surface Area of Room
Math Antics - Volume
Surface Area of a Square Pyramid | Math with Mr. J
Computing Surface areas using double integrals
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geome...
Area of a Circle | MathHelp.com
Area of a Trapezoid | MathHelp.com
Комментарии
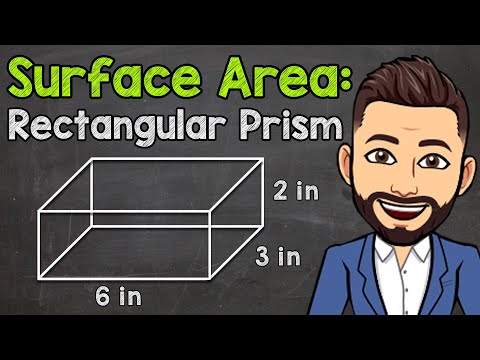 0:04:57
0:04:57
 0:04:06
0:04:06
 0:05:35
0:05:35
 0:08:22
0:08:22
 0:09:26
0:09:26
 0:10:26
0:10:26
 0:11:14
0:11:14
 0:30:36
0:30:36
 0:16:45
0:16:45
 0:08:07
0:08:07
 0:01:06
0:01:06
 0:05:39
0:05:39
 0:07:13
0:07:13
 0:03:28
0:03:28
 0:07:59
0:07:59
 0:07:56
0:07:56
 0:08:29
0:08:29
 0:09:09
0:09:09
 0:12:36
0:12:36
 0:08:42
0:08:42
 0:04:06
0:04:06
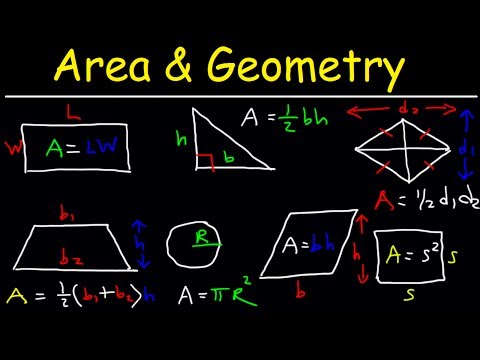 0:20:35
0:20:35
 0:01:40
0:01:40
 0:01:39
0:01:39