filmov
tv
The Surface Area formula for Parametric Surfaces // Vector Calculus

Показать описание
In this video we derive the formula to compute surface area given some surface described parametrically. Thus if you have a parametric description, all you need to do is plug it into this formula. The derivation works by looking at a tiny section of surface area, and approximating this with a little tangential parallelogram whose area can be computed by the length of the cross product of r_u Delta u and r_v Delta b, the partial derivatives of the position vector with respect to the two parameters u and v. Thus the integral is effectively just summing up these little surface areas and becomes a double integral of the length of that cross product. We will see a concrete example of this in the next video in the vector calculus playlit.
MY VECTOR CALCULUS PLAYLIST:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
MY VECTOR CALCULUS PLAYLIST:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
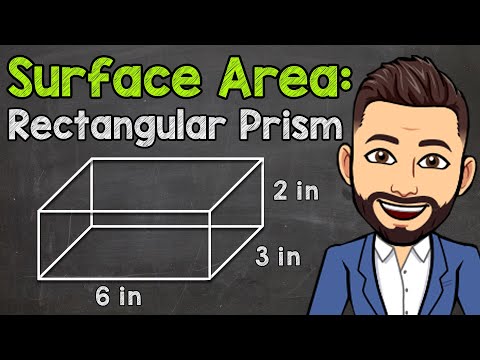
How to Find the Surface Area of a Rectangular Prism | Math with Mr. J
The Surface Area formula for Parametric Surfaces // Vector Calculus
Surface Area and Volume Review (Geometry)
But why is a sphere's surface area four times its shadow?
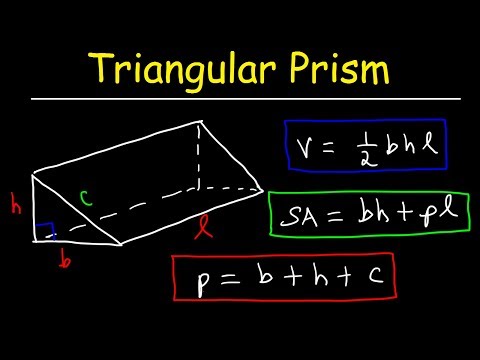
How to Find the Surface Area of a Triangular Prism | Math with Mr. J
How to Find the Surface Area of a Cylinder | Math with Mr. J
How to Find the Surface Area of a Cube | Math with Mr. J
What is the Surface Area of a Cylinder? | Don't Memorise
Formula Frenzy: Surface areas and Volumes of Cylinder, Sphere, Hemisphere and Cone.
Surface Area of Solid of Revolution (about x-axis, formula explained)
Easy math. Deriving the formula for the volume of a cone #ibmath #igcse #ibexam #math #ipmath
Volume of a Cylinder and Surface Area of a Cylinder
Surface Area | MathHelp.com
Math Antics - Area
Surface Area of a Cube
Area of Surfaces of Revolution | Derivation & Example
Formulas for area of 2D shapes // #shorts
What is Volume? | What is Surface Area? | Don't Memorise
Surface Area and Volume: Cube
Math Antics - Volume
What is the Surface Area of a Right Circular Cone? | Don't Memorise
Triangular Prism - Volume, Surface Area, Base and Lateral Area Formula, Basic Geometry
Surface Area of a Pyramid - Lateral Area - Geometry
Surface Area of Revolution By Integration Explained, Calculus Problems, Integral Formula, Examples
Комментарии
 0:04:57
0:04:57
 0:09:26
0:09:26
 0:16:51
0:16:51
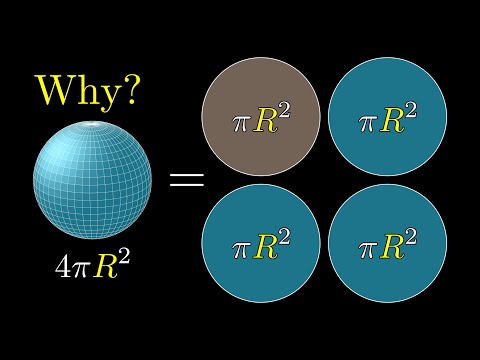 0:15:51
0:15:51
 0:06:42
0:06:42
 0:05:35
0:05:35
 0:04:06
0:04:06
 0:03:08
0:03:08
 0:01:01
0:01:01
 0:06:49
0:06:49
 0:00:48
0:00:48
 0:11:14
0:11:14
 0:02:45
0:02:45
 0:10:26
0:10:26
 0:01:42
0:01:42
 0:08:29
0:08:29
 0:00:44
0:00:44
 0:02:44
0:02:44
 0:04:33
0:04:33
 0:12:36
0:12:36
 0:04:34
0:04:34
 0:27:41
0:27:41
 0:03:28
0:03:28
 0:30:36
0:30:36