filmov
tv
Computing the Surface Area of an Implicitly Defined Surface

Показать описание
In this example, we compute the surface area using the formula for implicit surfaces that we talked about in the previous video of my vector calculus playlist (link below). This paraboloid could be tackled a few ways (parametrically, implicitly or explicitly), but we are going to use the implicit formula thinking of this surface as being above the xy-plane. The double integral that we get actually turns out to be easier to compute in polar coordinates so we make that conversion as well.
MY VECTOR CALCULUS PLAYLIST:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
MY VECTOR CALCULUS PLAYLIST:
OTHER COURSE PLAYLISTS:
OTHER PLAYLISTS:
► Learning Math Series
►Cool Math Series:
BECOME A MEMBER:
MATH BOOKS & MERCH I LOVE:
SOCIALS:
Computing the Surface Area of a surface parametrically // Example 1 // Vector Calculus
Computing the Surface Area of an Implicitly Defined Surface
Computing the Surface Area of a surface parametrically // Example 2 // Vector Calculus
Surface Area and Volume: Cylinder
Area of Surfaces of Revolution | Derivation & Example
The Surface Area formula for Parametric Surfaces // Vector Calculus
Math Antics - Circles, Circumference And Area
Surface Area for Implicit & Explicit Surfaces // Vector Calculus
Math Antics - Area
Evaluating Surface Integrals
Surface area of a box using nets
Area of a Rectangle, Triangle, Circle & Sector, Trapezoid, Square, Parallelogram, Rhombus, Geome...
Double integrals to find surface area (KristaKingMath)
Solving Surface Area & Volume of a Rectangular Prism | Math in Minutes
KutaSoftware: PreAlgebra- Surface Area
Calculating the Surface Area of a Rectangular Prism
Find Surface area of a solid object in autocad
Finding the Perimeter and Area of a Composite Shape | L-Shaped Example | Geometry | Math with Mr. J
Math Antics - Volume
Area of a Triangle | MathHelp.com
Example: Surface Area of a Plane
Surface Area of Room
Computing the Flux Across a Surface // Vector Calculus
Calculus 2: Area of a Surface of Revolution (Video #9) | Math with Professor V
Комментарии
 0:08:22
0:08:22
 0:07:13
0:07:13
 0:08:07
0:08:07
 0:01:06
0:01:06
 0:08:29
0:08:29
 0:09:26
0:09:26
 0:07:56
0:07:56
 0:08:13
0:08:13
 0:10:26
0:10:26
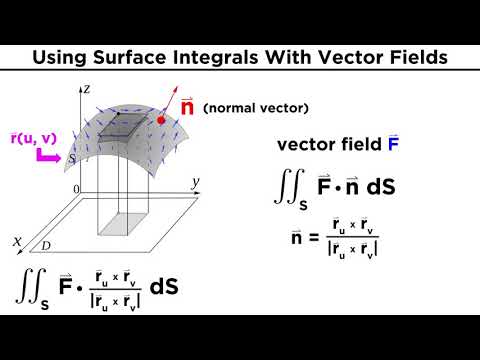 0:12:24
0:12:24
 0:04:43
0:04:43
 0:20:35
0:20:35
 0:12:12
0:12:12
 0:03:34
0:03:34
 0:44:52
0:44:52
 0:07:29
0:07:29
 0:00:29
0:00:29
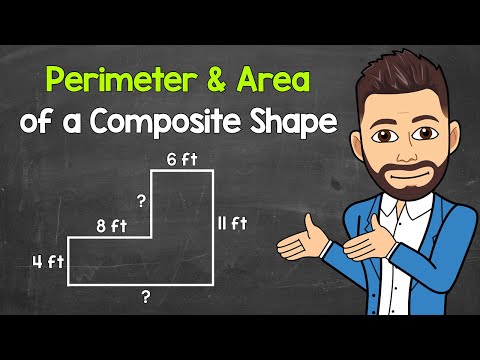 0:08:21
0:08:21
 0:12:36
0:12:36
 0:01:36
0:01:36
 0:05:18
0:05:18
 0:09:09
0:09:09
 0:08:09
0:08:09
 0:29:32
0:29:32