filmov
tv
Find the Sum of this Infinite Series | No Calculators Allowed! | Train Your Brain

Показать описание
#OlympiadMathematics #OlympiadPreparation #CollegeEntranceExam
What is the sum of 3/4 and 2/3?
How to find the sum of 3 numbers
Find the sum of the following fractions
Find the Sum of the Series SUM((2^n + 1)/3^n)
How To Derive The Formula For The Sum of an Arithmetic Series
Finding The Sum of an Infinite Geometric Series
How to find the sum of a mixed number and a fraction
How to use the SUM function in Microsoft Excel
5 Essential Excel Functions for Beginners
Sum and Difference
How To Find The Sum of a Geometric Series
Can You Find the Sum of the Infinite Series? | Learn How!
Finding the Sum of a Series by Differentiating
Finding the sum or an arithmetic series using summation notation
Math tutorial for determining the sum of an arithmetic series
How to Use Sum Function in Excel
SUM OF ARITHMETIC PROGRESSION (A.P)
How to Find the Sum of Functions | Algebra, Adding Functions, Sums of Functions
Find the Sum || Class -5 || Chapter Fraction || Farha Zakir
C Program To Find Sum of Series 1/1! + 2/2! + 3/3! + .... + n/n!
How to Find the Sum of odd Numbers - Using Sum of N terms Formula of Arithmetic Series
Find the Sum of the First 30 Terms of the Arithmetic Sequence 3, 7, 11, 15, ...
Learn how to find the sum of an arithmetic series
Find 3 Consecutive Even Integers with a Sum of 72
Комментарии
 0:03:05
0:03:05
 0:01:04
0:01:04
 0:03:20
0:03:20
 0:03:57
0:03:57
 0:06:38
0:06:38
 0:19:50
0:19:50
 0:01:55
0:01:55
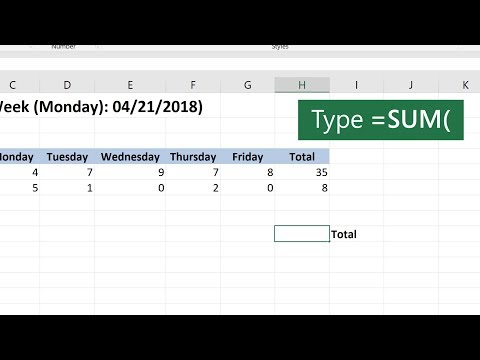 0:00:38
0:00:38
 0:01:00
0:01:00
 0:01:36
0:01:36
 0:05:14
0:05:14
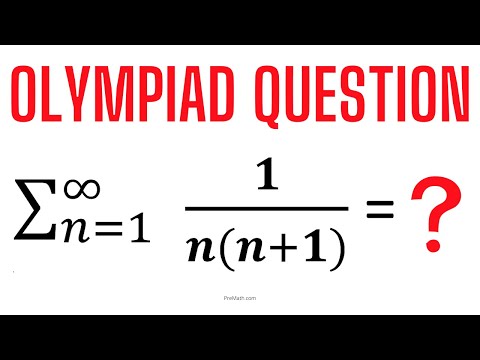 0:10:29
0:10:29
 0:04:01
0:04:01
 0:03:53
0:03:53
 0:06:37
0:06:37
 0:00:19
0:00:19
 0:04:50
0:04:50
 0:04:28
0:04:28
 0:04:40
0:04:40
 0:03:53
0:03:53
 0:04:12
0:04:12
 0:03:38
0:03:38
 0:07:11
0:07:11
 0:01:36
0:01:36