filmov
tv
Can You Find the Sum of the Infinite Series? | Learn How!
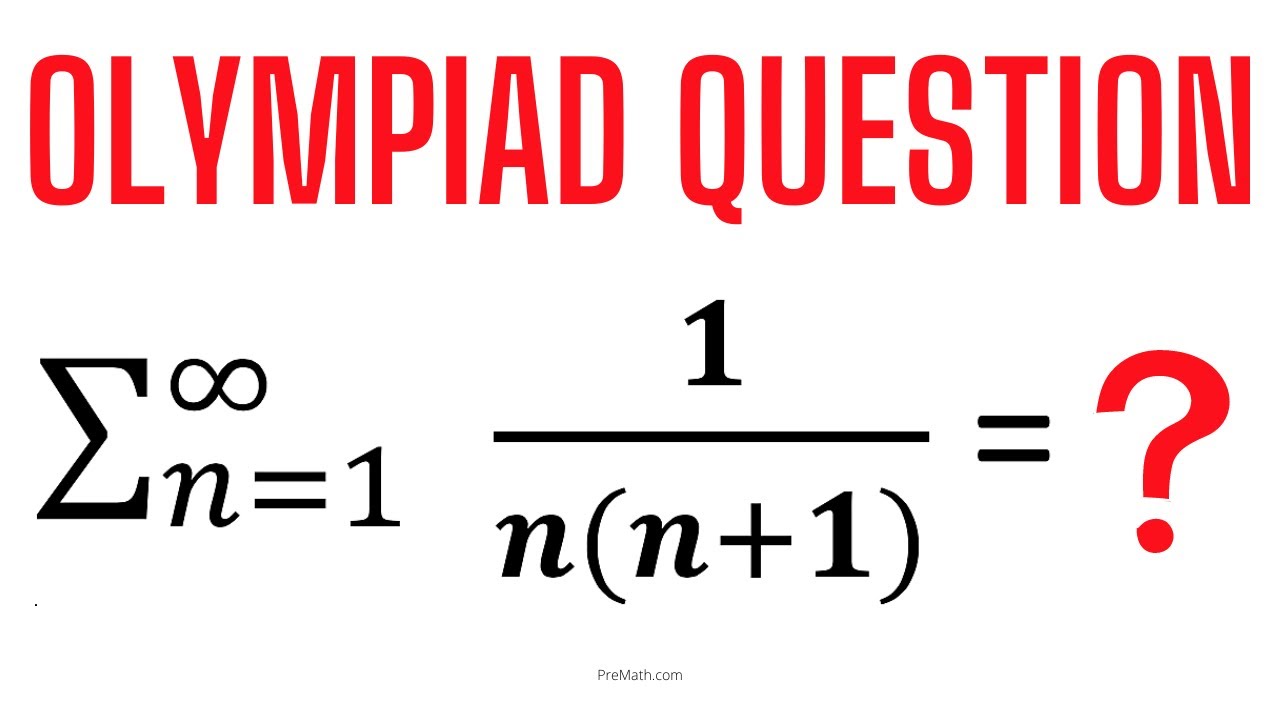
Показать описание
#OlympiadMathematics #OlympiadPreparation #CollegeEntranceExam
How to find the sum of 3 numbers
What is the sum of 3/4 and 2/3?
Can You Find the Sum of the Infinite Series? | Learn How!
Can you find two numbers whose sum is 18 and whose difference is 4? Math Word Problem!
Sum of natural numbers 1 to 100
Sum and Difference
How to use the SUM function in Microsoft Excel
Calculate the total sum of numbers | 684 number puzzle | How many numbers can you see?
CHALLENGE: Can you find digits A, B, and C???
Finding The Sum of an Infinite Geometric Series
Finding the sum or an arithmetic series using summation notation
Find the Sum of the Series by using Maclaurin Series
Find the sum of the following fractions
How to find the sum of a mixed number and a fraction
How To Find The Sum of a Geometric Series
How to Find the Sum of Functions | Algebra, Adding Functions, Sums of Functions
How To Find All Combinations That Equal A Given Sum In Excel
Find the Sum of the Series SUM((2^n + 1)/3^n)
Find sum of all digits in a number | Basic Math algorithm
Sum of 3 odd numbers equal to 30 | Find numbers from 1,3,5,7,9,11,13,15 to make sum 30
Learn how to determine the sum of a geometric finite series
How to Find the Exact Sum of a Series using Taylor Series | Series | Calculus | Glass of Numbers
Find the Sum of the First 30 Terms of the Arithmetic Sequence 3, 7, 11, 15, ...
How To Find Three Consecutive Integers With A Given Sum
Комментарии
 0:01:04
0:01:04
 0:03:05
0:03:05
 0:10:29
0:10:29
 0:08:18
0:08:18
 0:02:26
0:02:26
 0:01:36
0:01:36
 0:00:38
0:00:38
 0:02:11
0:02:11
 0:06:58
0:06:58
 0:19:50
0:19:50
 0:03:53
0:03:53
 0:03:11
0:03:11
 0:03:20
0:03:20
 0:01:55
0:01:55
 0:05:14
0:05:14
 0:04:28
0:04:28
 0:05:14
0:05:14
 0:03:57
0:03:57
 0:08:48
0:08:48
 0:01:23
0:01:23
 0:02:42
0:02:42
 0:14:55
0:14:55
 0:03:38
0:03:38
 0:03:55
0:03:55