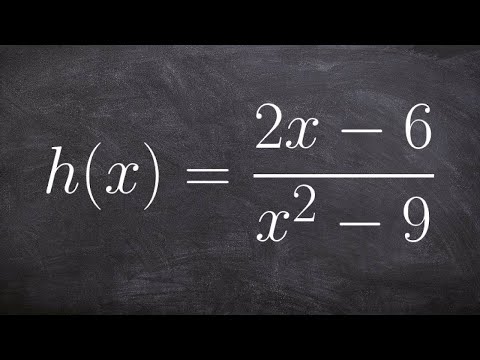filmov
tv
How to find the vertical and horizontal asymptotes of a function

Показать описание
👉 Learn how to find the vertical/horizontal asymptotes of a function. An asymptote is a line that the graph of a function approaches but never touches. The vertical asymptote is a vertical line that the graph of a function approaches but never touches. To find the vertical asymptote(s) of a rational function, we set the denominator equal to 0 and solve for x.
The horizontal asymptote is a horizontal line which the graph of the function approaches but never crosses (though they sometimes cross them). A rational function has a horizontal asymptote of y = 0 when the degree of the numerator is less than the degree of the denominator. A rational function has a horizontal asymptote of y = c, (where c is the quotient of the leading coefficient of the numerator and that of the denominator) when the degree of the numerator is equal to the degree of the denominator. A rational function has no horizontal asymptote if the degree of the numerator is greater than the degree of the denominator.
Organized Videos:
✅ Find the Asymptotes of Rational Functions
✅ Find the Vertical and Horizontal Asymptotes of a Rational Function y=0
✅ Asymptotes of Rational Functions | Learn About
✅ Find the Asymptotes of a Rational Function with Trig
✅ Find the Asymptotes and Holes of a Rational Function
✅ Find the Slant Asymptotes of the Rational Function
Connect with me:
#asymptotes #functions #brianmclogan
The horizontal asymptote is a horizontal line which the graph of the function approaches but never crosses (though they sometimes cross them). A rational function has a horizontal asymptote of y = 0 when the degree of the numerator is less than the degree of the denominator. A rational function has a horizontal asymptote of y = c, (where c is the quotient of the leading coefficient of the numerator and that of the denominator) when the degree of the numerator is equal to the degree of the denominator. A rational function has no horizontal asymptote if the degree of the numerator is greater than the degree of the denominator.
Organized Videos:
✅ Find the Asymptotes of Rational Functions
✅ Find the Vertical and Horizontal Asymptotes of a Rational Function y=0
✅ Asymptotes of Rational Functions | Learn About
✅ Find the Asymptotes of a Rational Function with Trig
✅ Find the Asymptotes and Holes of a Rational Function
✅ Find the Slant Asymptotes of the Rational Function
Connect with me:
#asymptotes #functions #brianmclogan
Комментарии