filmov
tv
Proving Inequalities using Linear Algebra

Показать описание
We prove the inequality 6x^2 - 4xy + 9y^2 ≥ 0 by expressing 6x^2 - 4xy + 9y^2 in terms of matrices, and then using diagonalisation. It turns out that this method can be generalised.
Proving Inequalities using Linear Algebra
Proving Algebraic Inequalities (1 of 3: Introductory principles)
Induction with inequalities
Visual Cauchy-Schwarz Inequality
Triangle Inequality for Real Numbers Proof
Proof of the Cauchy-Schwarz inequality | Vectors and spaces | Linear Algebra | Khan Academy
When mathematicians get bored (ep1)
How to prove inequalities using a basic one.
Math Proof Writing: Inequality Proof
Oxford student reacts to India’s JEE Advanced exam paper *really hard* #shorts #viral #jeeadvanced
Basic Cauchy-Schwarz Inequality - Linear Algebra Made Easy (2016)
Introduction to Inequality Proofs
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
the real reason why you're bad (or good) at math
Discrete Math - 5.1.2 Proof Using Mathematical Induction - Inequalities
That's Why Mohit Sir Called 'God Of Mathematics'| Puzzle Brain teaser | #competishun ...
Vector triangle inequality | Vectors and spaces | Linear Algebra | Khan Academy
Proving an Inequality Using Inequalities
Linear Algebra, Lesson 5, Video 16: Proof of Triangle Inequality
Logical Reasoning???#viral #vidumzn
Proving Inequalities
Linear Inequalities: Proving Solutions Mathematically
How REAL Men Integrate Functions
Quick Cauchy Schwarz Proof
Комментарии
 0:12:32
0:12:32
 0:09:37
0:09:37
 0:04:07
0:04:07
 0:01:01
0:01:01
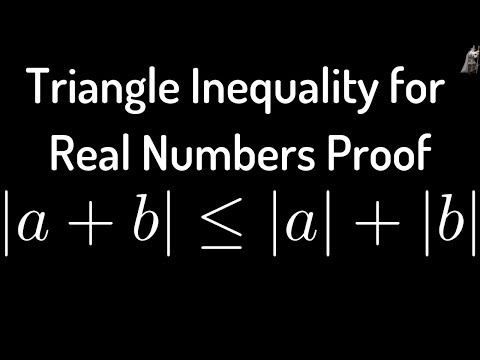 0:03:08
0:03:08
 0:16:55
0:16:55
 0:00:37
0:00:37
 0:00:30
0:00:30
 0:03:28
0:03:28
 0:01:00
0:01:00
 0:02:19
0:02:19
 0:12:05
0:12:05
 0:00:38
0:00:38
 0:00:59
0:00:59
 0:09:53
0:09:53
 0:00:19
0:00:19
 0:18:53
0:18:53
 0:14:50
0:14:50
 0:13:28
0:13:28
 0:00:11
0:00:11
 0:15:24
0:15:24
 0:05:19
0:05:19
 0:00:35
0:00:35
 0:04:53
0:04:53