filmov
tv
A Nice Radical System

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #RadicalSystems
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #RadicalSystems
EXPLORE 😎:
PLAYLISTS 🎵 :
A Nice Radical System
Solving a Nice Radical System in Two Ways
Solving A Nice Radical System in Two Ways
A Nice Radical Equation Solved in Three Ways
A Nice Radical System | Math Olympiads
India | A Nice Radical Equation
A Nice Radical Equation with Fifth Root
A Nice System of Radical Equations | Math Olympiad Preparation
Solving For A Nice Function
A Nice Radical Expression
Simplifying a Nice Radical Expression With Integers
A nice radical question step by step solution @mathscuriosity494
A Nice Radical Expression
A Nice Infinite Radical
Simplifying A Nice Radical Expression
A radical system of equations
A Nice Radical Equation
Solve This Equation for a | Equation Solving | A Nice Radical Equation
A Radical Idea: Solving A Homemade Radical System
Math Olympiad Question. A Nice Radical problem X^1/4=𝑿/𝟒. Simplify radical Expression
Simplifying a Nice Radical Expression in Two Ways
Solving A Nice Radical Equation | (√x+5)—(√4x+9)=–2 | Solution To Radical Equations | Math Tricks....
A Nice Interesting Algebraic Radical Math Problem. #shorts #maths #olympiad #mathematics #mathtricks
Solving A Nice Radical Equation | sqrt(x+5)=5–sqrt(x) | Radical Equations |Solving Radical Equations...
Комментарии
 0:08:48
0:08:48
 0:09:12
0:09:12
 0:09:46
0:09:46
 0:08:51
0:08:51
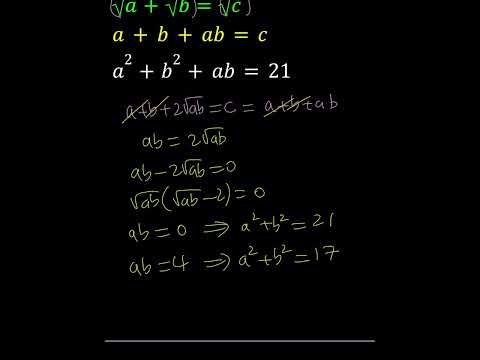 0:00:41
0:00:41
 0:11:35
0:11:35
 0:08:49
0:08:49
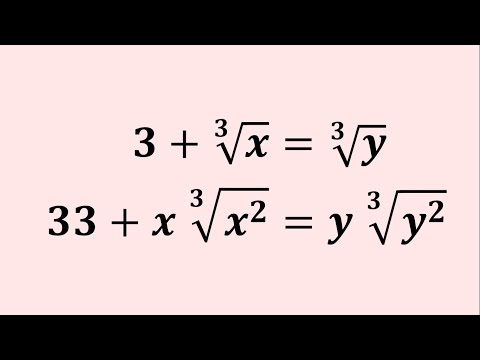 0:16:52
0:16:52
 0:08:39
0:08:39
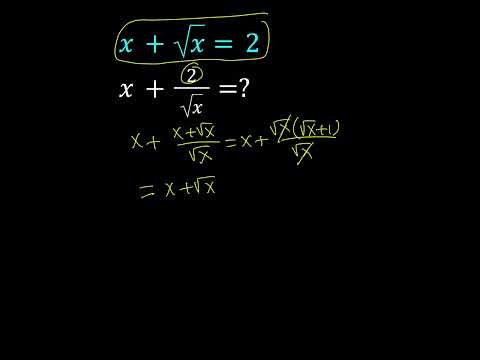 0:00:44
0:00:44
 0:06:38
0:06:38
 0:06:09
0:06:09
 0:08:27
0:08:27
 0:02:59
0:02:59
 0:00:39
0:00:39
 0:11:58
0:11:58
 0:06:26
0:06:26
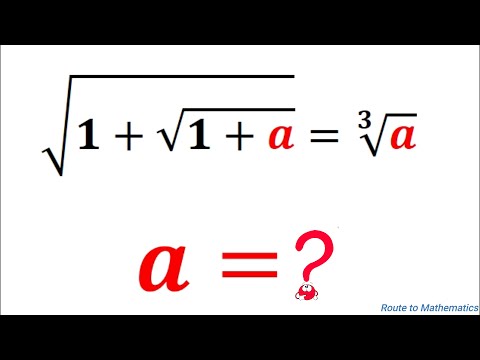 0:06:10
0:06:10
 0:05:36
0:05:36
 0:04:57
0:04:57
 0:11:44
0:11:44
 0:13:15
0:13:15
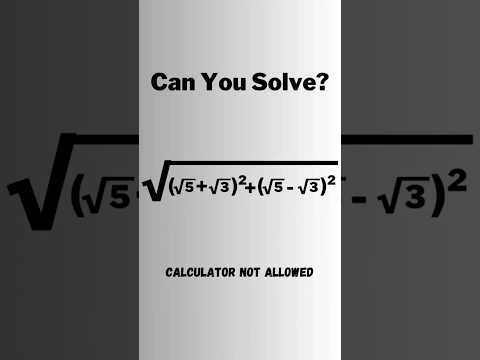 0:00:46
0:00:46
 0:12:08
0:12:08