India | A Nice Radical Equation

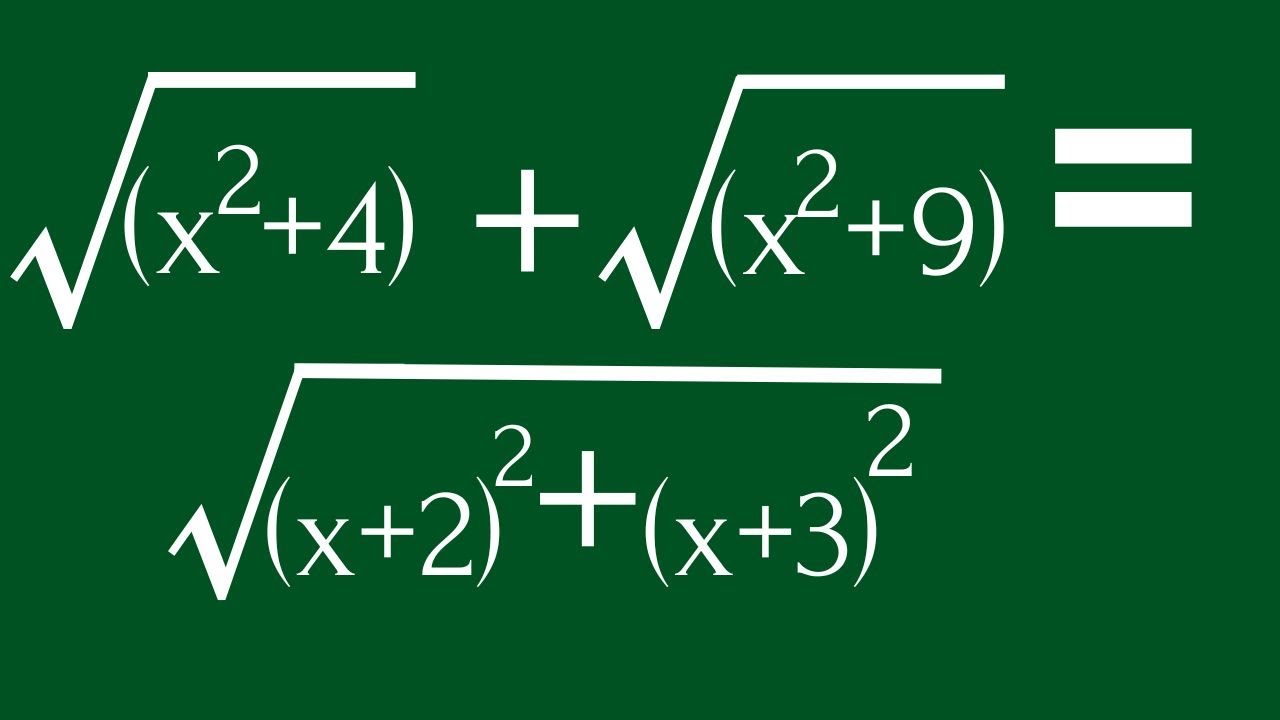
preview_player
Показать описание
Hello, here is another video for us to learn from.

Subscribe to our channel for more videos

Comment and share via the link;

Thanks to you all

#maths #education #educational #educationalvideo #educationalvideos #educationalvideos #educationmatters #educationalcontent #trending #trendingmaths #trendingvideo #trendingstatus #mathematics #mathstricks #math #mathematicsclasses #mathematic #solver #school #solution #solutionsmaster #solutions #sol #matholympiad #mathshorts #mathproblem #mathpuzzle #mathproblems #how #howto #onlineclasses #online #onlinelearning #common #commonentranceexam #testy #top #top10 #toptrending #onlinemaths #onlineclass #onlinemathstv
  1. OnlineMaths TV
  2. India
  3. A Nice Radical equation
  4. A Nice Radical Equation
  5. Cambridge Common entrance exam
  6. Cambridge University exam
Рекомендации по теме
India | A 0:11:35

India | A Nice Radical Equation

India || A 0:03:20

India || A Nice Radical Maths simplification || Maths Olympiad

Orthodox Christian Priest 0:00:17

Orthodox Christian Priest against radical islamist militias ☦️☦️☦️

Math Olympiad Challenge 0:07:43

Math Olympiad Challenge | A Nice Radical Problem

Indian Olympiads Entrance 0:08:20

Indian Olympiads Entrance Examination | Nice Radical Problem | No Calculator Allowed

Piers Gets in 0:06:18

Piers Gets in a Furious Debate on Whether or Not Men Can Be Mothers | Good Morning Britain

A Nice Math 0:04:32

A Nice Math radical problem| what is the value of k| Math Olympiad

radical equation challenge 0:01:58

radical equation challenge 🤯 __ nice Olympiad problem

Bangladesh's Expansionist Dreams: 0:03:12

Bangladesh's Expansionist Dreams: Radical Islamic Forces Pose Growing Threat to India's Bo...

A Nice Radical 0:02:13

A Nice Radical Problem 🔥 Math Olympiad | which is larger

Math Olympiad📌 | 0:10:11

Math Olympiad📌 | A Nice Radical Problem👌💯 | Can You Solve This ? ✔

Nice Exponent Problem 0:00:49

Nice Exponent Problem | Nice Radical Problem | how to make base same and eliminate negative exponent

INDIAN Math Olympiad 0:10:50

INDIAN Math Olympiad | Can You Solve This Radical Equation |

A Nice Radical 0:00:50

A Nice Radical Problem | BODMAS #shorts #olympiad #mathematics #maths #matholympiad #radical #tips

Mexico - A 0:05:09

Mexico - A Nice Math Olympiad Radical Problem #education #mathematics

A Nice Math 0:00:36

A Nice Math Problem With Fractional Radical Index. #shorts #maths #radical #olympiad #mathematics

A Nice Radical 0:06:09

A Nice Radical Expression | Can You Simplify

A Nice Radical 0:00:41

A Nice Radical System | Math Olympiads

A Nice Radical 0:00:35

A Nice Radical Problem √27+√12=? #shorts #maths #olympiad #mathematics #matholympiad #tips #radical...

Impact on India-UK 0:04:24

Impact on India-UK Ties: Sunak's Push for Radical Action and Visa Rule Changes

A Nice Squarer 0:00:53

A Nice Squarer Root Simplification Maths Problem. #shorts #maths #radical #squareroot #olympiad #yt

The Hardest Math 0:00:28

The Hardest Math Test

A Nice Radical 0:05:25

A Nice Radical Problem | Can you Solve this ? #premath #maths

Anant Ambani & 0:00:48

Anant Ambani & Radhika pre-wedding #shorts #anantambani #radhikamerchant radical #ambaniweddin...

Комментарии
Автор

Thank you my friend for your entertaining, sympathetic way of solving math exercises. Have a good weekend.

ElvisSaturn
Автор

Wonderful work through sir. Thanks so much for a job well done. More success sir...❤❤

danielfranca
Автор

Parfait 👍👍👍..belle continuation 🌹🙏🇩🇿🇩🇿🇩🇿🇩🇿

aines
Автор

Thank you for explaining. I think the solution is only x=√6 . 　I checked and I got to know "-√6 cannot satisfy the given equation."
Actually, [ if x=√6, (the left side) = √(6+4)+√(6+9) = √10+√15, and (the right side) = √((√6+2)^2+(√6+3)^2) = √(25+10√6) = √15+√10 . (OK) ]
if x=-√6, (the left side) = √(6+4)+√(6+9) = √10+√15, but (the right side) = √((-√6+2)^2+(-√6+3)^2) = √(25-10√6) = √15-√10 .
Thus, if x=-√6, (the left side) ≠ (the right side) . Therefore, the solution is only x=√6.

sy
Автор

please can you plug in /6 in the equation to show it's true

henrynwabueze
Автор

thank you, well done, i made the test successfully)

MeinhartKöster
Автор

2x² + 13 + 2√[(x² + 4)(x² + 9)]
= (x + 2)² + (x + 3)²

2x² + 13 + 2√(x⁴ + 13x² + 36) = 2x² + 13 + 10x

√(x⁴ + 13x² + 36) = 5x
x⁴ - 12x² + 36 = 0
(x² - 6)² = 0 => x = ± √6

VERIFICATION

x = √6
√10 + √15 = √(10 + 15 + 10√6)
√5(√2 + √3) = √(25 + 10√6)
√5(√2 + √2) = √5√(5 + 2√6)
√5(√2 + √3) = √5(√2 + √3) [ TRUE ]

x = -√6
√10 + √15 = √(10 + 15 - 10√6)
√5(√2 + √3) = √(25 - 10√6)
√5(√2 + √2) = √5√(5 - 2√6)
√5(√2 + √3) = √5(-√2 + √3) [ FALSE ]

*x = √6*

SidneiMV