filmov
tv
A Nice Radical Equation Solved in Three Ways

Показать описание
If you need to post a picture of your solution or idea:
#ChallengingMathProblems #RadicalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
#ChallengingMathProblems #RadicalEquations
EXPLORE 😎:
PLAYLISTS 🎵 :
A Nice Radical Equation | You Should Try it! | Math Olympiad Preparation
Solving Radical Equations
Solving A Nice Radical Equation | How To Solve Radical Equation With Two Radicals.
A Nice Radical Equation Solved in Three Ways
Solving radical equations | Exponent expressions and equations | Algebra I | Khan Academy
Solving a Radical Equation Using Factoring and Checking Your Answers
Can You Solve This Radical Equation? Math Olympiad Preparation
Solving A Nice Radical Equation | (√x+5)—(√4x+9)=–2 | Solution To Radical Equations | Math Tricks....
Solving Radical Equations #maths #shorts #algebra #algebratips #square #mathseducation
Solving Radical Equations With Square Roots, Cube Roots, Two Radicals, Fractions, Rational Exponents
05 - Solving Radical Equations & Identifying Extraneous Solutions - Part 1
Solving a nice radical equation
Solve This Equation for a | Equation Solving | A Nice Radical Equation
Solving Radical Equations
Solving A Nice Radical Equation
A Nice Radical Equation Solving | Math Olympiad Question | Only 7% Solved Using This Trick
India | A Nice Radical Equation
Math Tutorial for Solving Radical Equations
Solving A Nice Radical Equation | sqrt(x+5)=5–sqrt(x) | Radical Equations |Solving Radical Equations...
#9. Solve the Radical Equation with Two Square Roots
A nice Radical Equation | Math Olympiad | Algebra Problem | Find Real Value of 'x' ?
#maths | Solving A Nice Radical Equation | #algebra #youtubevideos
Solving A Radical Equation | Algebra
Solving a Nice Radical Equation in Two Ways
Комментарии
 0:00:00
0:00:00
 0:17:11
0:17:11
 0:19:51
0:19:51
 0:08:51
0:08:51
 0:03:11
0:03:11
 0:04:25
0:04:25
 0:13:56
0:13:56
 0:13:15
0:13:15
 0:01:01
0:01:01
 0:18:05
0:18:05
 0:27:27
0:27:27
 0:09:04
0:09:04
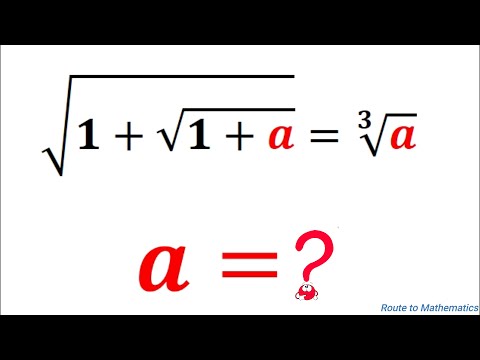 0:06:10
0:06:10
 0:03:31
0:03:31
 0:00:38
0:00:38
 0:05:45
0:05:45
 0:11:35
0:11:35
 0:03:45
0:03:45
 0:12:08
0:12:08
 0:05:17
0:05:17
 0:14:38
0:14:38
 0:06:02
0:06:02
 0:00:38
0:00:38
 0:11:59
0:11:59