filmov
tv
How to find second derivatives using implicit differentiation

Показать описание
When you take the derivative of a function, you are finding the rate of change of that function. The second derivative is simply the derivative of the derivative, or the rate of change of the rate of change. One way to find the second derivative is using implicit differentiation. This method involves taking derivatives while treating one variable as if it were a constant. For example, let's say you have the equation x^2+y^2=1. To find the second derivative with respect to x, we would first take the derivative of both sides with respect to x. This would give us 2x+2yy'=0. Then, we would take the derivative again, this time with respect to y. This would give us 2yy'+2x+2y'^2=0. Finally, we would solve for y''. In this case, we would get y''=-(2x+2y'^2)/(2y). Using implicit differentiation, we were able to find the second derivative without having to find an explicit formula for y in terms of x. This method can be useful when working with complex equations where it is difficult to solve for one variable in terms of another. In this video, we'll go through some easy steps you can use to find second derivatives implicitly
 0:02:26
0:02:26
 0:12:48
0:12:48
 0:07:03
0:07:03
 0:12:16
0:12:16
 0:10:51
0:10:51
 0:17:10
0:17:10
 0:07:04
0:07:04
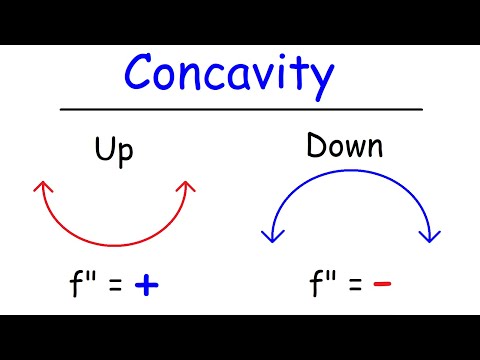 0:12:49
0:12:49
 0:14:51
0:14:51
 0:06:29
0:06:29
 0:04:29
0:04:29
 0:04:47
0:04:47
 0:05:20
0:05:20
 0:09:38
0:09:38
 0:04:33
0:04:33
 0:10:54
0:10:54
 0:07:02
0:07:02
 0:06:22
0:06:22
 0:07:04
0:07:04
 0:06:06
0:06:06
 0:07:29
0:07:29
 0:08:07
0:08:07
 0:17:30
0:17:30
 0:14:35
0:14:35