filmov
tv
second derivative of an ellipse, by using implicit differentiation

Показать описание
second derivative of an ellipse, by using implicit differentiation, calculus 1 tutorial
second derivative of an ellipse, by using implicit differentiation
Implicit 2nd Derivative of Elipse
Implicit Differentiation of an Ellipse
Calculus - Implicit Differentiation of an Ellipse
How REAL Men Integrate Functions
Derivative of a Horizontal Ellipse
Derivative for Horizontal Tangent on Ellipse
Second Derivative Implicitly | Calculus 1 Exercises
Example of Finding a Normal Line to an Ellipse
Difference Between Partial and Total Derivative
Impilicit Differentiation #shorts
Why greatest Mathematicians are not trying to prove Riemann Hypothesis? || #short #terencetao #maths
Second derivative of 9x^2+y^2=9 with implicit differentiation
Slope of an ellipse.
Tangents to an ellipse
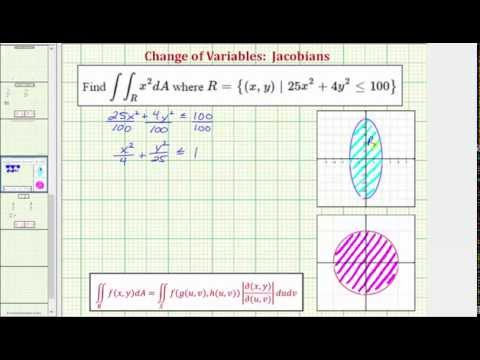
Evaluate a Double Integral of x^2 Over an Ellipse Using a Change of Variables (Jacobian, Polar)
Tangent Line with Implicit Differentiation | Calculus 1
10-2A Derivation of the Ellipse Formula
Deriving the Equation for an Ellipse
IIT Hostel Life | Padhne Wale BARISH mein bhi padh lete 😂 #iitdelhi #iit #iitbombay
Derivative of a Vertical Ellipse
1st yr. Vs Final yr. MBBS student 🔥🤯#shorts #neet
y = -x^2 + 3, find the first and second derivative
Functions IIT Questions NO 11 ( X Class)
Комментарии
 0:06:46
0:06:46
 0:07:18
0:07:18
 0:10:32
0:10:32
 0:04:54
0:04:54
 0:00:35
0:00:35
 0:06:52
0:06:52
 0:05:22
0:05:22
 0:07:02
0:07:02
 0:05:09
0:05:09
 0:01:44
0:01:44
 0:00:59
0:00:59
 0:00:38
0:00:38
 0:06:00
0:06:00
 0:06:51
0:06:51
 0:14:59
0:14:59
 0:09:39
0:09:39
 0:08:23
0:08:23
 0:39:10
0:39:10
 0:05:48
0:05:48
 0:00:29
0:00:29
 0:08:35
0:08:35
 0:00:20
0:00:20
 0:00:49
0:00:49
 0:00:48
0:00:48