filmov
tv
Linear Algebra 11L: The Three Equivalent Perspectives on Matrix Multiplication

Показать описание
Linear Algebra 11L: The Three Equivalent Perspectives on Matrix Multiplication
Cross products in the light of linear transformations | Chapter 11, Essence of linear algebra
Linear transformations and matrices | Chapter 3, Essence of linear algebra
Linear Algebra - Matrix Operations
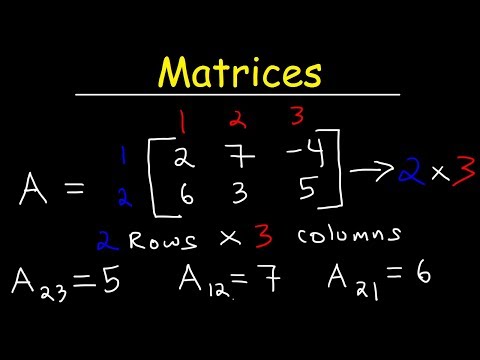
Intro to Matrices
Linear Algebra 11 | Matrices
Matrix multiplication as composition | Chapter 4, Essence of linear algebra
Determinant of 3x3 Matrices, 2x2 Matrix, Precalculus Video Tutorial
Linear Transformations with Calculus | Linear Algebra
The determinant | Chapter 6, Essence of linear algebra
Eigenvectors and eigenvalues | Chapter 14, Essence of linear algebra
Row Echelon Form of the Matrix Explained | Linear Algebra
Linear Algebra 11 | Matrices [dark version]
Linear combinations, span, and basis vectors | Chapter 2, Essence of linear algebra
Vectors | Chapter 1, Essence of linear algebra
Linear Algebra: Ch 2 - Determinants (22 of 48) The Cofactor of a Matrix
Sarrus Rule | How To Fast Calculate The Determinant of A 3 x 3 Matrix | Linear Algebra
Cramer's rule, explained geometrically | Chapter 12, Essence of linear algebra
Three-dimensional linear transformations | Chapter 5, Essence of linear algebra
Algebra 43 - Types of Linear Systems in Three Variables
Solving Matrix Equations
Inverse matrices, column space and null space | Chapter 7, Essence of linear algebra
Applications of 3x3 matrices | Wild Linear Algebra A 11 | NJ Wildberger
Multiplying Matrices
Комментарии
 0:09:03
0:09:03
 0:13:10
0:13:10
 0:10:59
0:10:59
 0:07:08
0:07:08
 0:11:23
0:11:23
 0:10:14
0:10:14
 0:10:04
0:10:04
 0:10:17
0:10:17
 0:05:45
0:05:45
 0:10:03
0:10:03
 0:17:16
0:17:16
 0:11:11
0:11:11
 0:10:16
0:10:16
 0:09:59
0:09:59
 0:09:52
0:09:52
 0:04:13
0:04:13
 0:02:04
0:02:04
 0:12:12
0:12:12
 0:04:46
0:04:46
 0:07:25
0:07:25
 0:06:31
0:06:31
 0:12:09
0:12:09
 0:53:36
0:53:36
 0:17:40
0:17:40