filmov
tv
The Simplest Impossible Problem

Показать описание
A 7-year-old can understand this problem which completely baffles mathematicians.
The Simplest Impossible Problem
The Simplest Math Problem No One Can Solve - Collatz Conjecture
The Simplest Impossible Problem #shorts
The Riddle That Seems Impossible Even If You Know The Answer
Simple Principle Solves Seemingly IMPOSSIBLE Math Problems
The Impossible Problem NO ONE Can Solve (The Halting Problem)
This question is actually impossible
IMPOSSIBLE mate in 1?
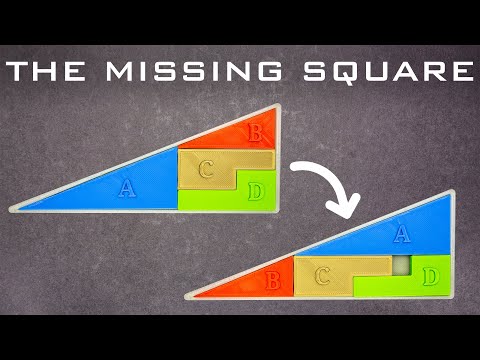
The IMPOSSIBLE Missing Square puzzle #short
impossible puzzle solved by easy way (no need to fold the paper)
Why this puzzle is impossible
How to Solve Impossible Puzzle
Challenge Your Brain with Pen & Paper Game - Impossible Pattern Solving Puzzle #shorts
I FINALLY Solved Baldi's Impossible Question... (and it was so simple...)
The impossible chessboard puzzle
An Impossible Perpetual Motion Device?! 😳 #Shorts
This math problem is impossible 😱 #shorts
Why is this 15-Puzzle Impossible? - Numberphile
The secret to Baldi's Impossible question......😲
Impossible Tiktok Towel Challenge Solved!! (Solution) #Shorts
The Halting Problem - An Impossible Problem to Solve
This was IMPOSSIBLE! 👀🤭🤣 | Triple Charm #shorts
The Impossible Checkmate? (mate in 2)
1150. Impossible Math Problem
Комментарии
 0:03:57
0:03:57
 0:22:09
0:22:09
 0:00:53
0:00:53
 0:17:45
0:17:45
 0:15:50
0:15:50
 0:20:24
0:20:24
 0:05:55
0:05:55
 0:00:45
0:00:45
 0:00:45
0:00:45
 0:00:57
0:00:57
 0:19:37
0:19:37
 0:01:02
0:01:02
 0:00:43
0:00:43
 0:15:11
0:15:11
 0:18:42
0:18:42
 0:01:00
0:01:00
 0:00:45
0:00:45
 0:23:44
0:23:44
 0:00:09
0:00:09
 0:00:23
0:00:23
 0:07:37
0:07:37
 0:00:32
0:00:32
 0:00:59
0:00:59
 0:00:10
0:00:10