filmov
tv
Complex Analysis: sin(x)=pi
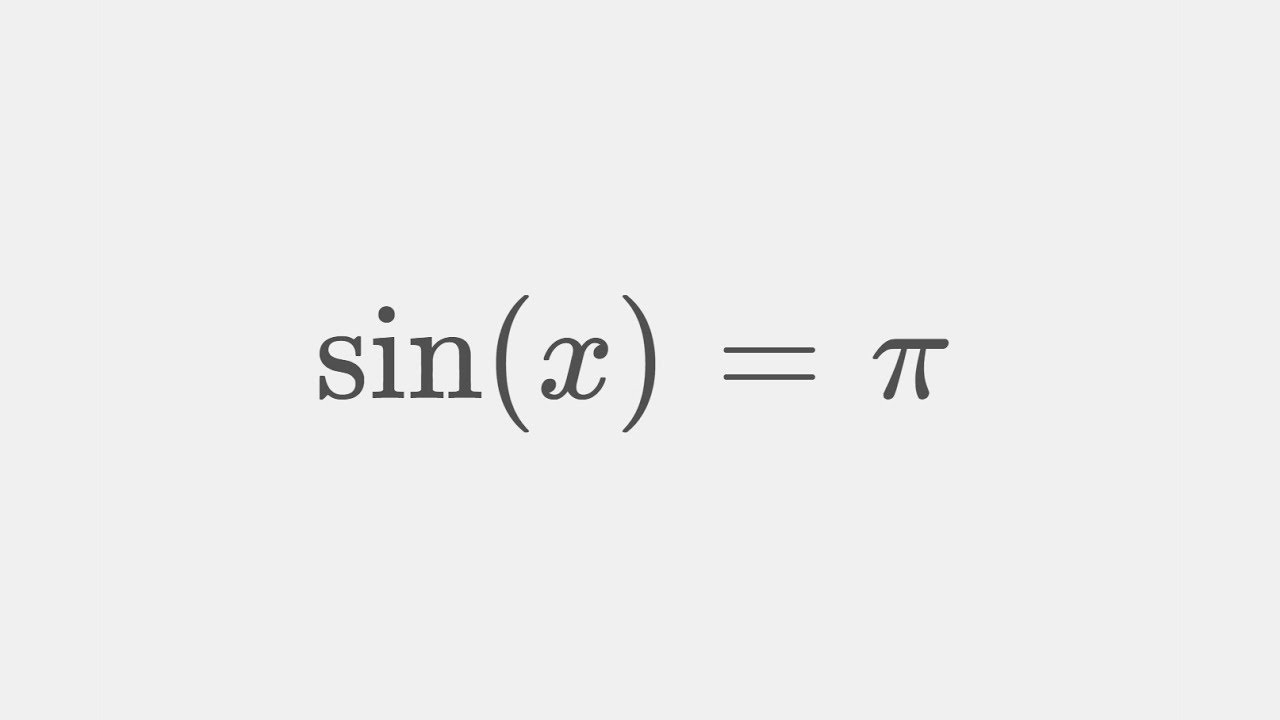
Показать описание
Help me create more free content! =)
Ever asked yourselve how to calculate the sine for complex values? Then here is your answer =)
Visit my website! =)
Complex Analysis: sin(x)=pi
Complex Analysis: Integral of sin(x)/x using Contour Integration
e^(iπ) in 3.14 minutes, using dynamics | DE5
The Dirichlet integral: integral of sinx/x from -ve to +ve infinity using contour integration
Complex sine function Sin ( pi + i Ln 3 ) Complex Analysis
Integral of sinx/x by Complex Analysis
A beautiful approach to the Fresnel integrals using complex analysis
Integral of sinx/x complex analysis close contour residus theorem
Definite Integrals #definiteintegrals #definiteintegral #integration
1.5 Minutes: Integral of |sin(x)| from -π/2 to π/2: Step-by-Step Calculus Tutorial
Taylor series | Chapter 11, Essence of calculus
How REAL Men Integrate Functions
The Sine Function: f(x) = sin(x)
Complex Analysis: Integral of xsin(x)/(x^2+1) using Contour Integration
Complex analysis: integral of cos(x^2), integral of sin(x^2) Fresnel integrals
Advance Calculus: Using complex analysis to evaluate this famous integral Sin(x)/x
Complex Analysis: Integral of log(sin(x))
Contour integration ( When poles lies on tha real axis)(Complex Analysis)
Contour Integration of functions having poles on the Real Axis (Complex Analysis)
Complex Analysis: Integral of (x-sin(x))/x^3
Complex Analysis | Unit 2 | Lecture 13 | Example of Cauchy's Integral Formula
GATE Taylor Series Example 2 Short Cut Trick Method Taylor series expansion of sin x about x=pi/6
Sine Curve and the Unit Circle
IIT Bombay CSE 😍 #shorts #iit #iitbombay
Комментарии
 0:15:57
0:15:57
 0:17:43
0:17:43
 0:04:08
0:04:08
 0:15:37
0:15:37
 0:07:18
0:07:18
 0:11:27
0:11:27
 0:06:59
0:06:59
 0:18:14
0:18:14
 0:16:01
0:16:01
 0:01:27
0:01:27
 0:22:20
0:22:20
 0:00:35
0:00:35
 0:05:35
0:05:35
 0:17:37
0:17:37
 0:09:30
0:09:30
 0:21:00
0:21:00
 0:33:30
0:33:30
 0:14:24
0:14:24
 1:04:10
1:04:10
 0:14:26
0:14:26
 0:09:05
0:09:05
 0:02:24
0:02:24
 0:00:27
0:00:27
 0:00:11
0:00:11