filmov
tv
Complex Analysis: Integral of sin(x)/x using Contour Integration
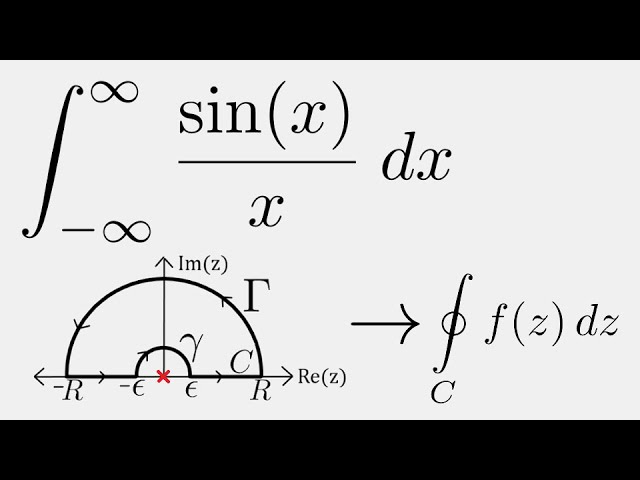
Показать описание
Today, we use complex analysis to evaluate the improper integral of sin(x)/x, also known as the Dirichlet Integral.
Laplace Transform Method:
Laplace Transform Method:
Complex Analysis: Integral of sin(x)/x using Contour Integration
The Dirichlet integral: integral of sinx/x from -ve to +ve infinity using contour integration
Advance Calculus: Using complex analysis to evaluate this famous integral Sin(x)/x
Integral of sinx/x complex analysis close contour residus theorem
Complex Analysis: Integral of (x-sin(x))/x^3
Integral of sinx/x by Complex Analysis
Complex Analysis: Integral of xsin(x)/(x^2+1) using Contour Integration
Let's do complex analysis: Integrating sin^2(x)/x^2(x^2+1) from 0 to infinity using residue the...
A beautiful result in calculus: Solution using complex analysis ( Integral cos(x)/(x^2+1) )
Complex Analysis: Integral of 1/(a+sin(x)) using Contour Integration
Contour integral: sinx/x integral from 0 to infinity
Complex definitions of sine and cosine
Contour integration ( When poles lies on tha real axis)(Complex Analysis)
DESTROYING THE DIRICHLET INTEGRAL (sin(x)/x) AND LETTING IT BURN IN THE 7th CIRCLE OF HELL
Complex analysis: integral of cos(x^2), integral of sin(x^2) Fresnel integrals
EX: The integral of sin(x) / x (part 1)
The Dirichlet Integral Marathon! int sinx/x from 0 to infty in 5 different ways
Contour Integration. Type : IV (Algebraic + Trigonometric Functions) in Complex Analysis.
Complex analysis integral of sin(x^2) fresnel integrals
Complex Analysis: Integral of sin(x^n)/x^n using Contour Integration
Destroying the Dirichlet integral using the Laplace transform (int sinx/x from -ve to +ve infty)
Fastest way to integrate sinx/x from zero to infty
EX: The integral of sin(x) / x (part 2)
A COMPLEX BOI! Integral sin(e^x) from -infinity to infinity using complex analysis
Комментарии
 0:17:43
0:17:43
 0:15:37
0:15:37
 0:21:00
0:21:00
 0:18:14
0:18:14
 0:14:26
0:14:26
 0:11:27
0:11:27
 0:17:37
0:17:37
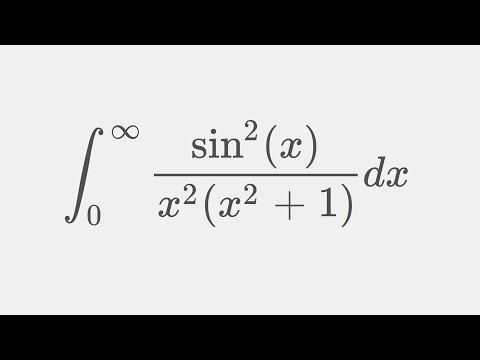 0:28:16
0:28:16
 0:16:40
0:16:40
 0:18:21
0:18:21
 0:06:13
0:06:13
 0:05:16
0:05:16
 0:14:24
0:14:24
 0:03:09
0:03:09
 0:09:30
0:09:30
 0:10:50
0:10:50
 0:29:54
0:29:54
 0:20:56
0:20:56
 0:07:48
0:07:48
 0:42:05
0:42:05
 0:06:46
0:06:46
 0:02:09
0:02:09
 0:09:33
0:09:33
 0:20:18
0:20:18